Please show your code. Any program works but prefer matlab

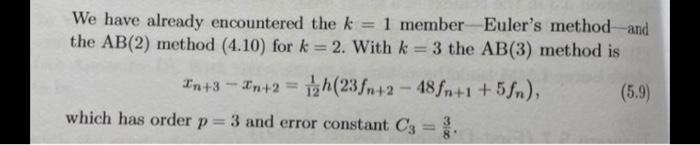
Implement the backward Euler method (Table 4.2 in text), the BDF2 (eqn 4.25 in text), and the Adams Bashforth 3 method (eqn. 5.9 in text) for solving the following initial value problems: 1. The Dahlquist test case: 'O X.r(t), 1 (0.5] x(0) 1. with X = -1, -10.-50 and h = 0.5, 0.1,0.01. 2. An oscillating coefficient test case cos(t) r(t), TE (0,01 (0) with h = 0.2.0.1,0.05,0.025 (here the exact solution is r(t) = exp(sin(O)). For both problems: 1. Calculate the maximum error and plot the computed solution(BE, BDF2, AB3) versus the true solution in all cases. 2. Discuss whether your results exhibit the expected stability and order of convergence for the various schemes. k 1 1 P 1 1 Method In +1 -In hfn Wn+1 - In = hfn+1 Name Euler Backward Euler 4.10.* Determine the order and error constant of the LMM 3n+2 - 4x +1 +In = 2h fn+2, (4.25) which is known as the "two-step backward differentiation formula": BDF(2) We have already encountered the k = 1 member Euler's method and the AB(2) method (4.10) for k = 2. With k =3 the AB(3) method is Un+3 -- Wn+2 = 1(23fn+2 - 48fn+1 +5fn), (5.9) which has order p=3 and error constant C3 Implement the backward Euler method (Table 4.2 in text), the BDF2 (eqn 4.25 in text), and the Adams Bashforth 3 method (eqn. 5.9 in text) for solving the following initial value problems: 1. The Dahlquist test case: 'O X.r(t), 1 (0.5] x(0) 1. with X = -1, -10.-50 and h = 0.5, 0.1,0.01. 2. An oscillating coefficient test case cos(t) r(t), TE (0,01 (0) with h = 0.2.0.1,0.05,0.025 (here the exact solution is r(t) = exp(sin(O)). For both problems: 1. Calculate the maximum error and plot the computed solution(BE, BDF2, AB3) versus the true solution in all cases. 2. Discuss whether your results exhibit the expected stability and order of convergence for the various schemes. k 1 1 P 1 1 Method In +1 -In hfn Wn+1 - In = hfn+1 Name Euler Backward Euler 4.10.* Determine the order and error constant of the LMM 3n+2 - 4x +1 +In = 2h fn+2, (4.25) which is known as the "two-step backward differentiation formula": BDF(2) We have already encountered the k = 1 member Euler's method and the AB(2) method (4.10) for k = 2. With k =3 the AB(3) method is Un+3 -- Wn+2 = 1(23fn+2 - 48fn+1 +5fn), (5.9) which has order p=3 and error constant C3