Please solve using MATLAB and post your script. Thank you!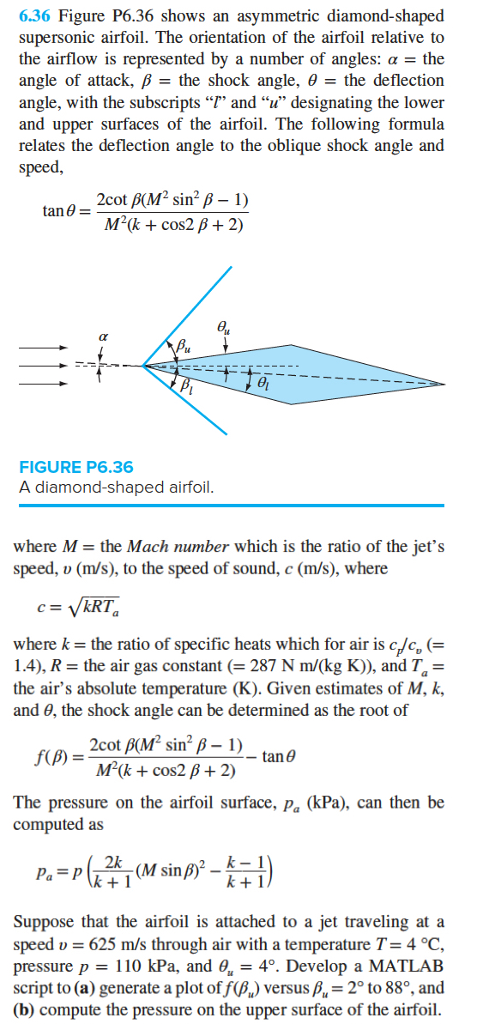

6.36 Figure P6.36 shows an asymmetric diamond-shaped supersonic airfoil. The orientation of the airfoil relative to the airflow is represented by a number of angles: = the angle of attack, -the shock angle, the deflection angle, with the subscripts , and "u designating the lower and upper surfaces of the airfoil. The following formula relates the deflection angle to the oblique shock angle and speed M2(k + cos2 + 2) FIGURE P6.36 A diamond-shaped airfoil where M the Mach nmnber which is the ratio of the jet's speed, v (m/s), to the speed of sound, c (m/s), where where the ratio of specific heats which for air is c/co (= 1.4), R = the air gas constant (= 287 N m/(kg K), and Ta = the air's absolute temperature (K). Given estimates of M, k, and , the shock angle can be determined as the root of tan M2(k + cos2 + 2) The pressure on the airfoil surface, pa (kPa), can then be computed as (M sinB2 Suppose that the airfoil is attached to a jet traveling at a speed u = 625 m/s through air with a temperture T= 4 C, pressure p = 110 kPa, and . = 4. Develop a MATLAB script to (a) generate a plot off.) versus ,-2 to 88, and (b) compute the pressure on the upper surface of the airfoil