Please stop reporting my question. I really need help :/

Hi,

I was wondering if someone could help me. I have completed the whole assignment but I got feedback and was wondering if someone could redo it so that it fits the feedback, most of it is correct and if possible to just read over this to make sure its following the provided instructions: To earn full marks, you must justify your solution. Include the following as needed: Show diagram, Define variables, State formula, theorem, equation or function used, Show substitutions and or steps in solving an equation, State restrictions, State concluding statement, Use correct notation. No marks are given if your solution includes: e or ln, differentiation, integration

I will also add the link to the doc so that you could mak e a copy and then edit and send it back so that its easier? thank you this would mean so much!

Heres the feedback I got: "you made 8 equations to satisfy the 8 parameters. Can you reduce that number of equations to 4 or less and reuse the same equation? e.g. Some equations can have a vertical asymptote, a y-intercept and a horizontal asymptote. Two of your formula's for the constraints are incorrect (They don't work). I won't tell you which two"

(Please fix the two as well)

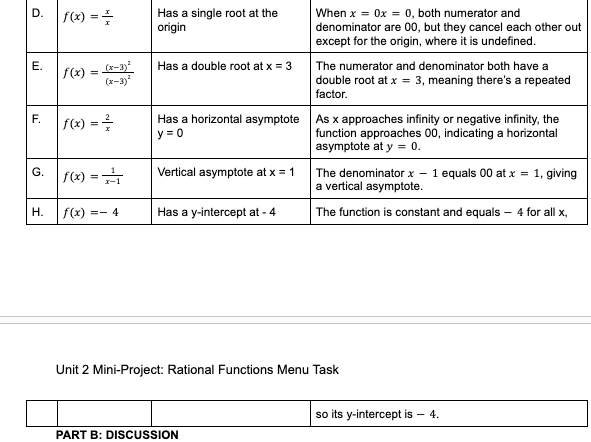
Unit 2 Mini-Project: Rational Functions Menu Task To earn full marks, you must justify your solution. Include the following as needed: Show diagram, Define variables, State formula, theorem, equation or function used, Show substitutions and or steps in solving an equation, State restrictions, State concluding statement, LIse correct notation. Mo marks are given if your solution includes: e or In, differentiation, integration PART A: THE FUNCTIONS Build as few rational functions as possible to satisfy each constraint at least once. Hasaholeatx=4 Has a double rootatx=-3 Vertical asymptote atx =- 2 _ Has a horizontal asymptote y = 0 Has a horizontal asymptote y = 2 G, Vertical asymptote at x = 1 m Has a single root at the origin Has a y-intercept at - 4 List all of your functions below and number them. Be sure to state which constraints they meet, and justify your choice. Has aholeatx =4 By factoring ' 16, we get(x 4)(x + 4). The factor (x 4) cancels out in the denominator, leaving a hole at x = 4. Vertical asymptote at x = -2 | The denominator x + 2 equals 00 at x which gives a vertical asymptote. Has a horizontal asymptote | The function is constant and its value is 22 for all x, =2 indicating a horizontal asymptote at y = 2. D. f (x) = Has a single root at the When x = 0x = 0, both numerator and origin denominator are 00, but they cancel each other out except for the origin, where it is undefined. E. f(x) = -3) Has a double root at x = 3 The numerator and denominator both have a (x-n) double root at x = 3, meaning there's a repeated factor. F. f(x) = Has a horizontal asymptote As x approaches infinity or negative infinity, the y= 0 function approaches 00, indicating a horizontal asymptote at y = 0. G. f(x) = Vertical asymptote at x = 1 The denominator x - 1 equals 00 at x = 1, giving a vertical asymptote. H. /(x) =- 4 Has a y-intercept at - 4 The function is constant and equals - 4 for all x, Unit 2 Mini-Project: Rational Functions Menu Task so its y-intercept is - 4. PART B: DISCUSSIONPART B: DISCUSSION Answer the following in complete sentences. Give full and complete explanations. Which constraints pair nicely? Constraints that pair nicely are those that do not conflict with each other and can coexist within the same rational function. o [For example: # Having a hole at x = 4 and having a double root at x = 3 can pair nicely because they are distinct points. * Having a vertical asymptote at = 2 and having a vertical asymptote at x = 1 can pair nicely because they occur at different locations on the x-axis. * Having horizontal asymptotes at y = 0 and = 2 can pair nicely because they are different horizontal lines. Which constraints cannot be paired? # Consfraints that cannot be paired are those that conflict with each other or are mutually exclusive within the same rational function. o [For example: # Having a single root at the origin and having a double root at x = 3 cannot be paired because a single root means one root, while a double root means two roots at the same paint. * Having a horizontal asymptote at v = 0 and having a y-intercept at 4 cannot be paired because the horizontal asymptote would prevent the function from intersecting the y-axis at 4. Is it possible to satisfy all constraints in 2, 3, or 4 rational functions? Some constraints are contradictory or mutually exclusive, so it is not possible to satisfy all of the constraints in just two rational functions. Nonetheless, depending on the exact armrangement of constraints and the functions used, it might be able to satisfy all constraints with just three or four rational functions. To make sure that every constraint is taken care of without interfering with the others, this would need considerable thought and analysis