Please use MATLAB for code

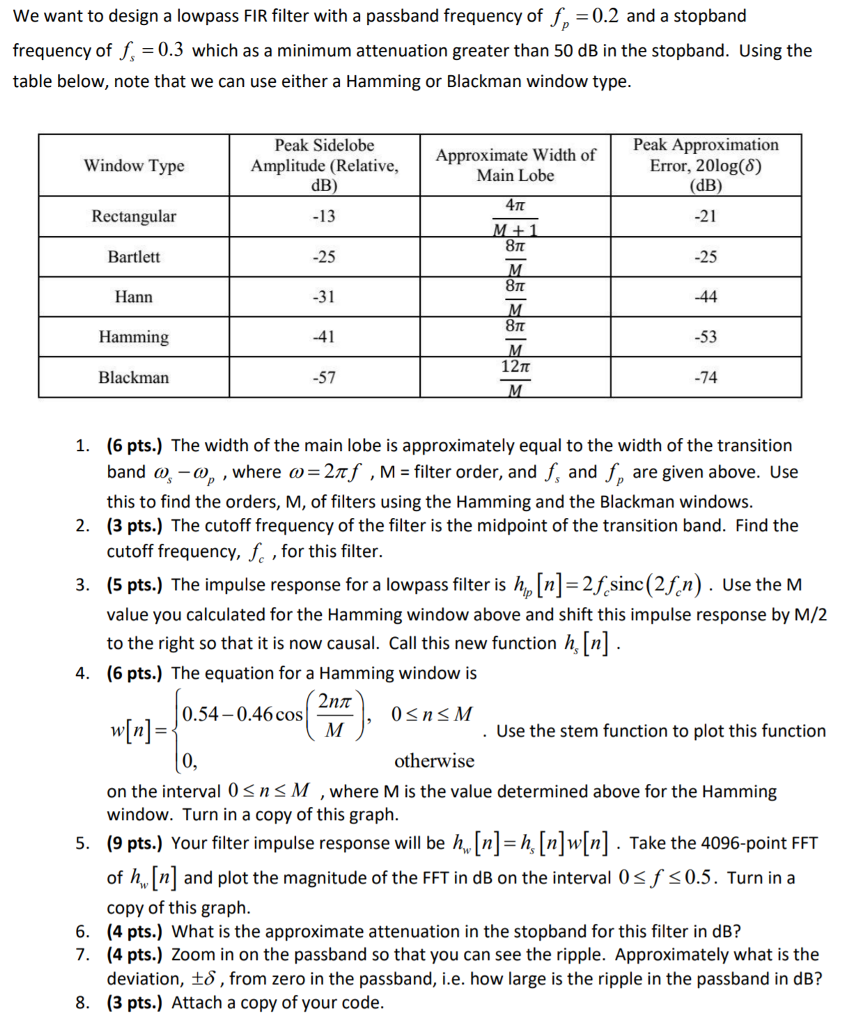
We want to design a lowpass FIR filter with a passband frequency of f 0.2 and a stopband frequency of f, -0.3 which as a minimum attenuation greater than 50 dB in the stopband. Using the table below, note that we can use either a Hamming or Blackman window type Peak Approximation Error, 20log(5) (dB) Peak Sidelobe Approximate Width of Main Lobe Window Type Amplitude (Relative., dB) Rectangular -21 25 -44 -53 -74 8? -25 -31 -41 -57 Bartlett Hamming 121t Blackman (6 pts.) The width of the main lobe is approximately equal to the width of the transition band a),-a)p , where ?-2zf , M filter order, and fs and fp are given above. Use this to find the orders, M, of filters using the Hamming and the Blackman windows (3 pts.) The cutoff frequency of the filter is the midpoint of the transition band. Find the cutoff frequency, f, for this filter. (5 pts.) The impulse response for a lowpass filter is n-2n(2f). Use the M value you calculated for the Hamming window above and shift this impulse response by M/2 to the right so that it is now causal. Call this new function h [n] . (6 pts.) The equation for a Hamming window is 1. 2. 4. 2nn 0.54-0.46 cos w[n] . Use the stem function to plot this function otherwise on the interval 0SnS M , where M is the value determined above for the Hamming window. Turn in a copy of this graph 5. (9 pts.) Your filter impulse response will be h nl-h[n|w[n|. Take the 4096-point FFT of h. [n] and plot the magnitude of the FFT in dB on the interval 0sf s0.5. Turn in a copy of this graph 6. (4 pts.) What is the approximate attenuation in the stopband for this filter in dB? 7. (4 pts.) Zoom in on the passband so that you can see the ripple. Approximately what is the deviation, t, from zero in the passband, i.e. how large is the ripple in the passband in dB? (3 pts.) Attach a copy of your code 8. We want to design a lowpass FIR filter with a passband frequency of f 0.2 and a stopband frequency of f, -0.3 which as a minimum attenuation greater than 50 dB in the stopband. Using the table below, note that we can use either a Hamming or Blackman window type Peak Approximation Error, 20log(5) (dB) Peak Sidelobe Approximate Width of Main Lobe Window Type Amplitude (Relative., dB) Rectangular -21 25 -44 -53 -74 8? -25 -31 -41 -57 Bartlett Hamming 121t Blackman (6 pts.) The width of the main lobe is approximately equal to the width of the transition band a),-a)p , where ?-2zf , M filter order, and fs and fp are given above. Use this to find the orders, M, of filters using the Hamming and the Blackman windows (3 pts.) The cutoff frequency of the filter is the midpoint of the transition band. Find the cutoff frequency, f, for this filter. (5 pts.) The impulse response for a lowpass filter is n-2n(2f). Use the M value you calculated for the Hamming window above and shift this impulse response by M/2 to the right so that it is now causal. Call this new function h [n] . (6 pts.) The equation for a Hamming window is 1. 2. 4. 2nn 0.54-0.46 cos w[n] . Use the stem function to plot this function otherwise on the interval 0SnS M , where M is the value determined above for the Hamming window. Turn in a copy of this graph 5. (9 pts.) Your filter impulse response will be h nl-h[n|w[n|. Take the 4096-point FFT of h. [n] and plot the magnitude of the FFT in dB on the interval 0sf s0.5. Turn in a copy of this graph 6. (4 pts.) What is the approximate attenuation in the stopband for this filter in dB? 7. (4 pts.) Zoom in on the passband so that you can see the ripple. Approximately what is the deviation, t, from zero in the passband, i.e. how large is the ripple in the passband in dB? (3 pts.) Attach a copy of your code 8