Question: pls help Suppose we define activity level as the number of calories burned in a single workout. We define a multiple linear regression model as

pls help

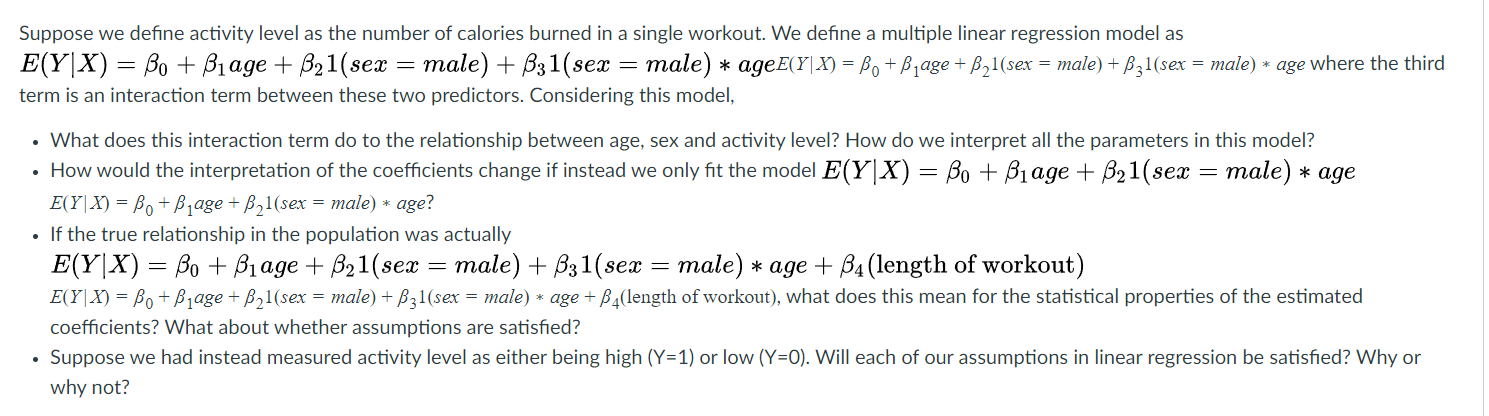
Suppose we define activity level as the number of calories burned in a single workout. We define a multiple linear regression model as E(Y X) = Bo + Biage + B21(sex = male) + 831(sex = male) * ageE(YIX) = Bo + Bjage + 821(sex = male) + 831(sex = male) * age where the third term is an interaction term between these two predictors. Considering this model, . What does this interaction term do to the relationship between age, sex and activity level? How do we interpret all the parameters in this model? . How would the interpretation of the coefficients change if instead we only fit the model E(Y| X) = Bo + Biage + B21(sex = male) * age E(Y X) = Bo + Bjage + B21(sex = male) * age? . If the true relationship in the population was actually E(Y X) = Bo + Biage + B21(sex = male) + 831(sex = male) * age + 84 (length of workout) E(Y X) = Bo+ Bjage + B21(sex = male) + 831(sex = male) * age + B4(length of workout), what does this mean for the statistical properties of the estimated coefficients? What about whether assumptions are satisfied? . Suppose we had instead measured activity level as either being high (Y=1) or low (Y=0). Will each of our assumptions in linear regression be satisfied? Why or why not

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

pls help Suppose we define activity level as the number of calories burned in a single workout. We define a multiple linear regression model as E(Y X) = Bo + Biage + B21(sex = male) + 831(sex = male)...

Suppose we define activity level as the number of calories burned in a single workout. We define a multiple linear regression model as E(Y X) = Bo + Biage + B21(sex = male) + 831(sex = male) *...

im so confuse for this question Suppose we define activity level as the number of calories burned in a single workout. We define a multiple linear regression model as E(Y X) = Bo + Biage + B21(sex =...

Please help answer any of the two questions below and explain in detail. Thank you! Suppose we define activity level as the number of calories burned in a single workout. We define a multiple linear...

Please answer any of the two questions in detail. Thank you. Suppose we define activity level as the number of calories burned in a single workout. We define a multiple linear regression model as...

Suppose we define activity level as the number of calories burned in a single workout. We define a multiple linear regression model as (|)=0+1+21(=)+31(=)E(Y|X)=0+1age+21(sex=male)+31(sex=male)age...

.... Kindly help me understand this problems only 12-106. + Consider the following computer output. (f) Plot the residuals versus y. Are there any indications of The regression equation is inequality...

Part c 12. When prices are (P1, P2)= (1,2), the consumer demands (X1, X2) = (1,2). When prices are (Q1, Q2) = (2,1), the consumer demands (Y1, Y2) = (2,1). Is this consumer behaviour consistent with...

Specification and Verification II Consider the following Verilog phrases: initial r = 0; always @(posedge clk) r = a + r; Write down a formula in logic that relates clk, a and r at a level of...

Brashear Inc. currently has $ 2,145,000 in current assets and $ 858,000 in current liabilities. The companys managers want to increase the firms inventory, which will be financed by a short- term...

1Part: Choose one of the topics presented in the transportation technology items from your textbook list it in youre and address the following: ?summarize the topic. ?locate a related news item on...

The slope of the characteristic line, which is estimated using statistical methods and shows the general relationship between a stock's return and the market's return, is called the beta.

A firm becomes more vertically integrated when . it buys a direct competitor d. it outsources some activities either upstream or downstream of its core business it competes in vertical industries its...

1. To gain insight into communication situations regarding the fact that they should be understood by examining the relationship between the parts and the whole, and to provide an understanding that...

2. Using a communication conflict you have been involved in, or a problem or phenomenon that you are familiar with, provide answers for a)d). a) Find the critical elements that existed (exist) as you...

5. What is meant by the statement, when we attribute a different meaning to a situation, the situation will consequentially change for us?