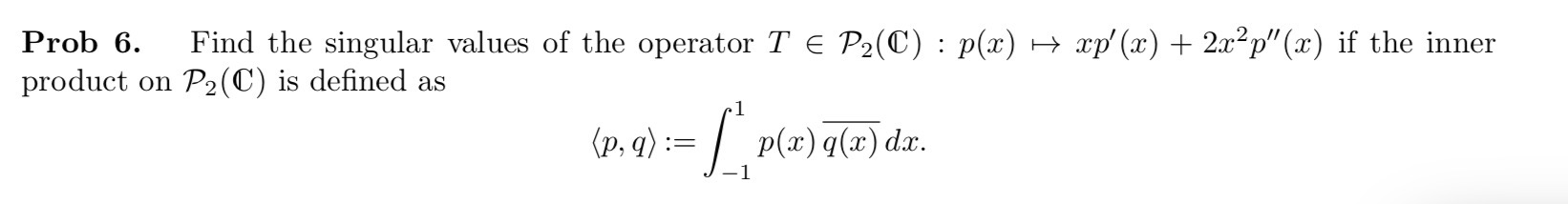
Prob 4. Show that the operator T = D2 is nonnegative on the space V :=span(1, cos cc,sin:c) over IR, with the inner product (f, g) := :f(x)g(m)dm. Find (a) its square root operator x/i (b) an example of a selfadjoint operator R 7E x/T such that R2 2 T; (c) an example of a nonselfadjoint operator 8 such that 8*8' = T. Prob 6. Find the singular values of the operator I ( P 2 ( [" ) : P ( 20 ) M acp' ( 20 ) + 2 202 p " ( 20 ) if the inner product on Pz ( [' ) is defined as ( P , 9 ) = = P ( 20 ) 9 ( ac ) doc