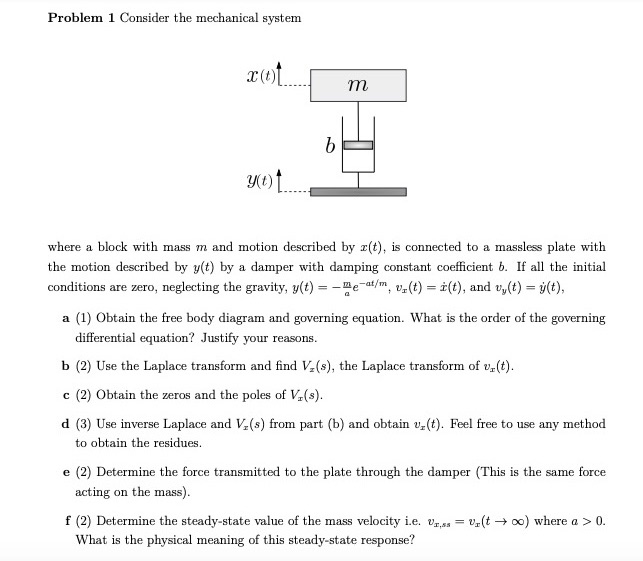
Problem 1 Consider the mechanical system x(+) m Y(t) b where a block with mass m and motion described by x(t), is connected to a massless plate with the motion described by y(t) by a damper with damping constant coefficient b. If all the initial conditions are zero, neglecting the gravity, y(t) = -eat/m, v(t)=(t), and v,(t) = y(t), a (1) Obtain the free body diagram and governing equation. What is the order of the governing differential equation? Justify your reasons. b (2) Use the Laplace transform and find V2(s), the Laplace transform of v(t). c (2) Obtain the zeros and the poles of V(s). d (3) Use inverse Laplace and V(s) from part (b) and obtain v,(t). Feel free to use any method to obtain the residues. e (2) Determine the force transmitted to the plate through the damper (This is the same force. acting on the mass). f (2) Determine the steady-state value of the mass velocity i.e. v = v(too) where a > 0. What is the physical meaning of this steady-state response?