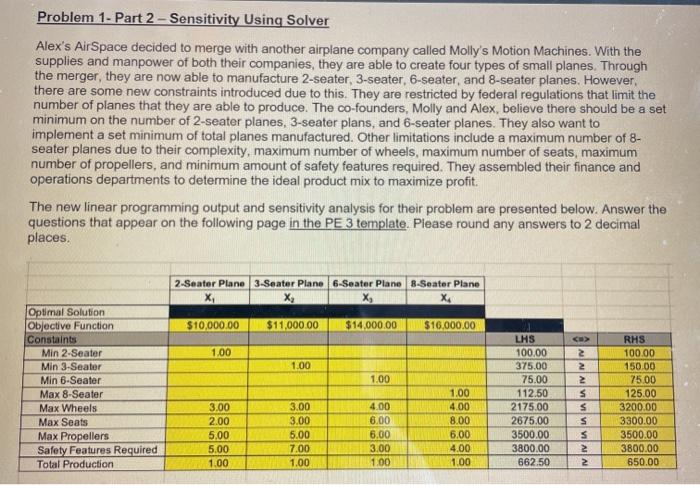
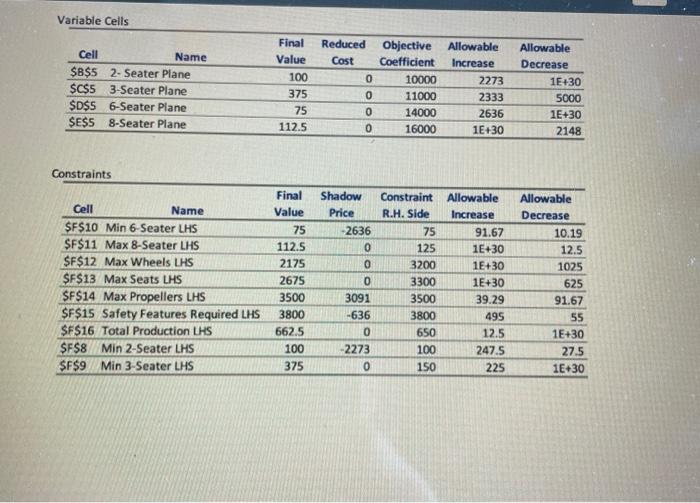
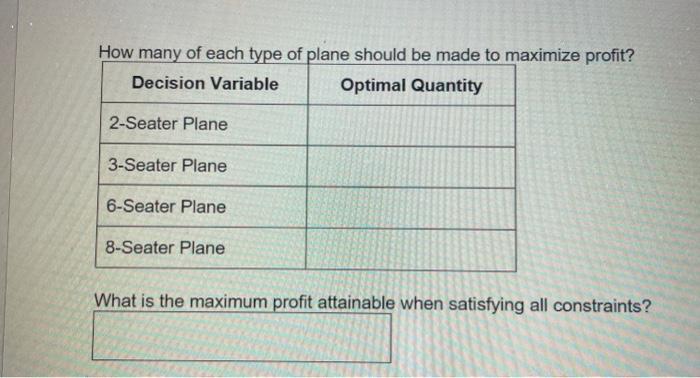
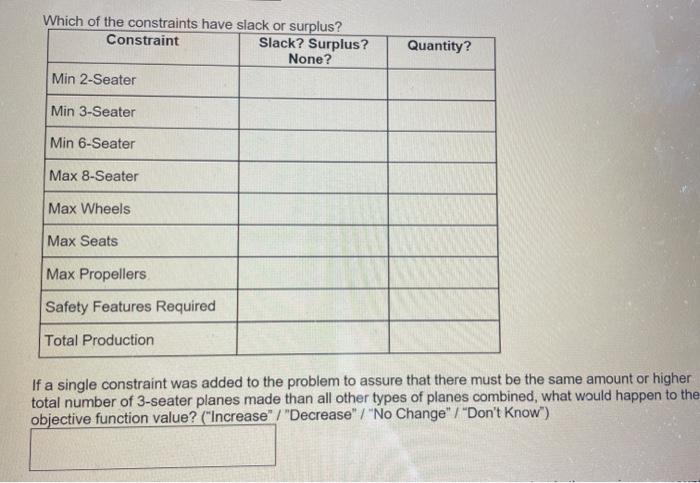
Problem 1- Part 2 - Sensitivity Using Solver Alex's Air Space decided to merge with another airplane company called Molly's Motion Machines. With the supplies and manpower of both their companies, they are able to create four types of small planes. Through the merger, they are now able to manufacture 2-seater, 3-seater, 6-seater, and 8-seater planes. However, there are some new constraints introduced due to this. They are restricted by federal regulations that limit the number of planes that they are able to produce. The co-founders, Molly and Alex, believe there should be a set minimum on the number of 2-seater planes, 3-seater plans, and 6-seater planes. They also want to implement a set minimum of total planes manufactured. Other limitations include a maximum number of 8- seater planes due to their complexity, maximum number of wheels, maximum number of seats, maximum number of propellers, and minimum amount of safety features required. They assembled their finance and operations departments to determine the ideal product mix to maximize profit The new linear programming output and sensitivity analysis for their problem are presented below. Answer the questions that appear on the following page in the PE 3 template. Please round any answers to 2 decimal places. 2-Seater Plane 3-Seater Plane 6-Seater Plane 8-Seater Plane X X, X X4 $10,000.00 $11,000.00 $14,000.00 $16,000.00 1.00 AININ 1.00 1.00 Optimal Solution Objective Function Constaints Min 2 Seater Min 3-Seater Min 6-Seater Max 8-Seater Max Wheels Max Seats Max Propellers Safety Features Required Total Production 3.00 2.00 5.00 5.00 1.00 3.00 3.00 5.00 7.00 1.00 LHS 100.00 375.00 75.00 112.50 2175.00 2675.00 3500.00 3800.00 662.50 RHS 100.00 150.00 7500 125.00 3200.00 3300.00 3500.00 3800.00 650.00 1.00 4.00 8.00 6.00 4.00 1.00 4.00 6.00 6.00 3.00 1.00 Variable Cells Cell Name $B$ 52- Seater Plane $C$5 3-Seater Plane $D$S 6-Seater Plane SESS 8-Seater Plane Final Value 100 375 75 112.5 Reduced Objective Allowable Cost Coefficient Increase 0 10000 2273 0 11000 2333 0 14000 2636 0 16000 1E+30 Allowable Decrease 1E+30 5000 1E+30 2148 Constraints Cell Name $F$10 Min 6-Seater LHS $F$11 Max 8-Seater LHS $F$12 Max Wheels LHS $F$13 Max Seats LHS $F$14 Max Propellers LHS $F$15 Safety Features Required LHS $F$16 Total Production LHS $F$8 Min 2-Seater LHS $F$9 Min 3-Seater LHS Final Value 75 112.5 2175 2675 3500 3800 662.5 100 375 Shadow Price 2636 0 0 0 3091 -636 0 -2273 0 Constraint R.H. Side 75 125 3200 3300 3500 3800 650 100 150 Allowable Increase 91.67 1E+30 1E+30 1E+30 39.29 495 12.5 247.5 225 Allowable Decrease 10.19 12.5 1025 625 91.67 55 1E+30 27.5 1E+30 How many of each type of plane should be made to maximize profit? Decision Variable Optimal Quantity 2-Seater Plane 3-Seater Plane 6-Seater Plane 8-Seater Plane What is the maximum profit attainable when satisfying all constraints? Which of the constraints have slack or surplus? Constraint Slack? Surplus? None? Quantity? Min 2-Seater Min 3-Seater Min 6-Seater Max 8-Seater Max Wheels Max Seats Max Propellers Safety Features Required Total Production If a single constraint was added to the problem to assure that there must be the same amount or higher total number of 3-seater planes made than all other types of planes combined, what would happen to the objective function value? ("Increase" / "Decrease" / "No Change" / "Don't Know") Max Seats Page