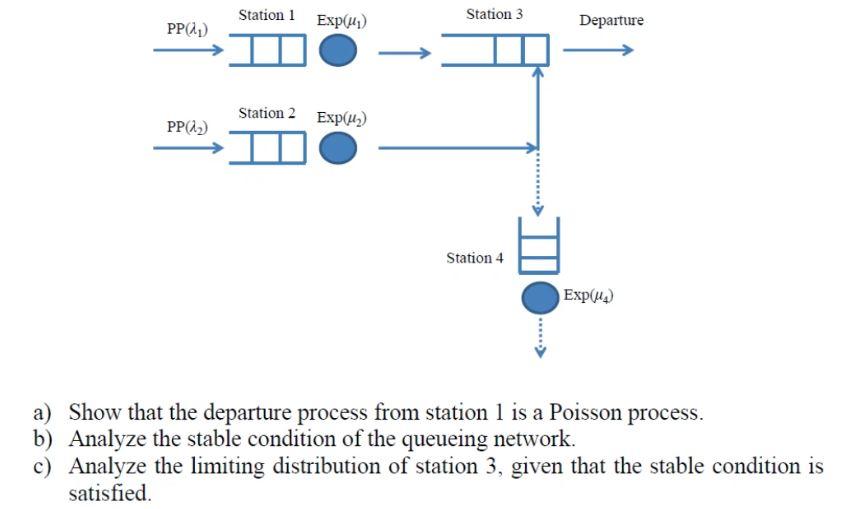
Question: Problem 1: Two kinds of raw materials arrive at two manufacturing stations following Poisson processes with rates and in, which have a single machine producing

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


