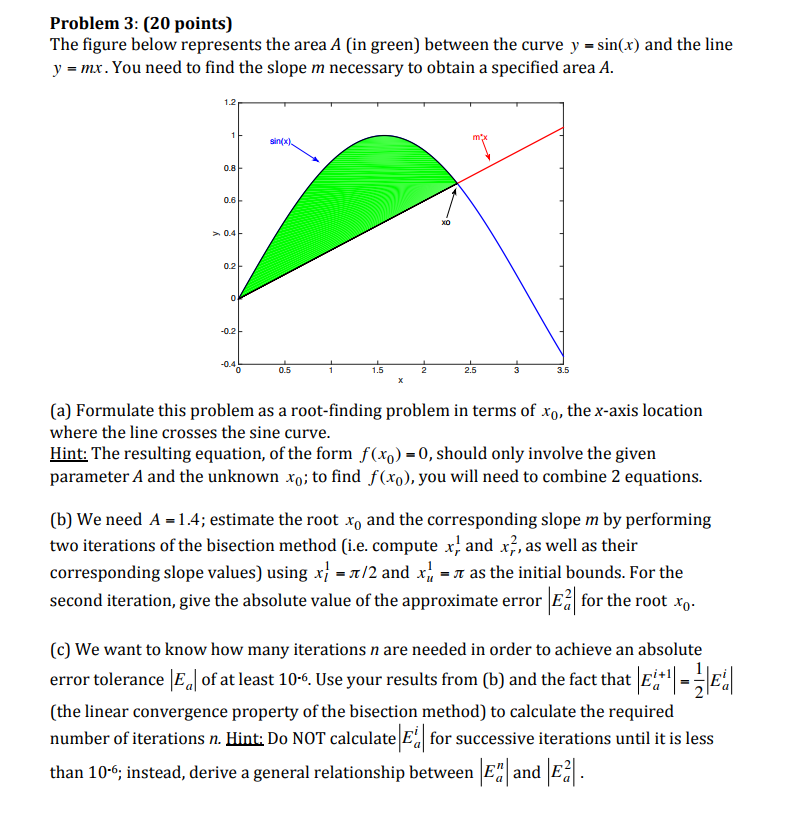
Problem 3: (20 points) The figure below represents the area A (in green) between the curve y - sin(x) and the line y - mx. You need to find the slope m necessary to obtain a specified area A. 1.2 0.8 0.6 0.4 0.2 0.2 0.5 2.5 3.5 (a) Formulate this problem as a root-finding problem in terms of xo, the x-axis location where the line crosses the sine curve Hint: The resulting equation, of the form f(xo) 0, should only involve the given parameter A and the unknown xo; to find f(xo), you will need to combine 2 equations. (b) We need A-1.4; estimate the root xo and the corresponding slope m by performing two iterations of the bisection method (i.e. compute xf and x?, as well as their corresponding slope values) using x-/2 and x"-r as the initial bounds. For the second iteration, give the absolute value of the approximate error Ea for the root xo (c) We want to know how many iterations n are needed in order to achieve an absolute error tolerance Ea of at least 10-6. Use your results from (b) and the fact that EE (the linear convergence property of the bisection method) to calculate the required number of iterations n. Hint. Do NOT calculate E for successive iterations until it is less than 10-6; instead, derive a general relationship between Ea dEa