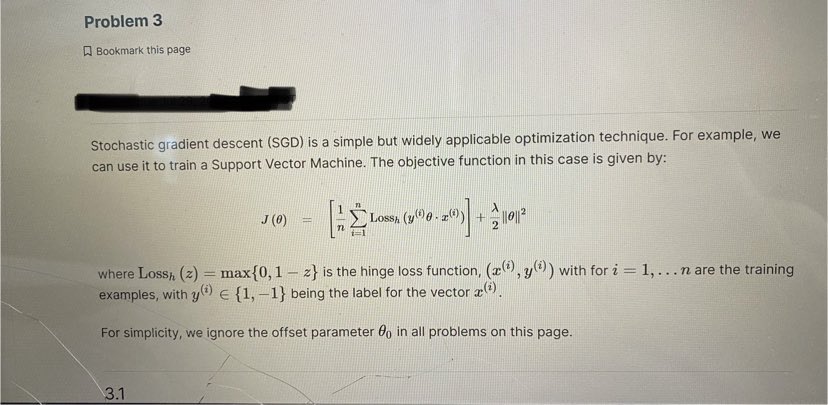
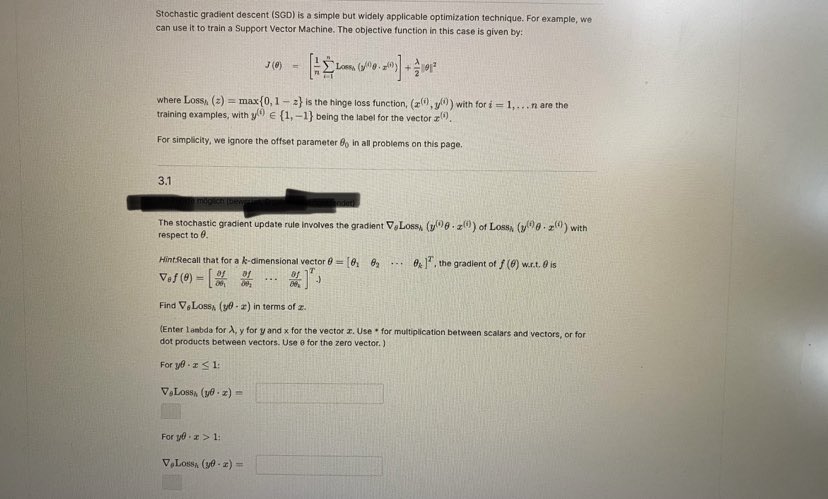
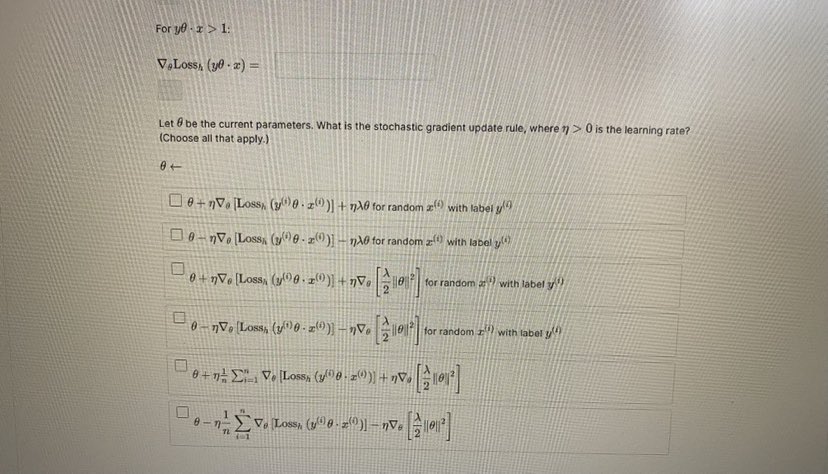
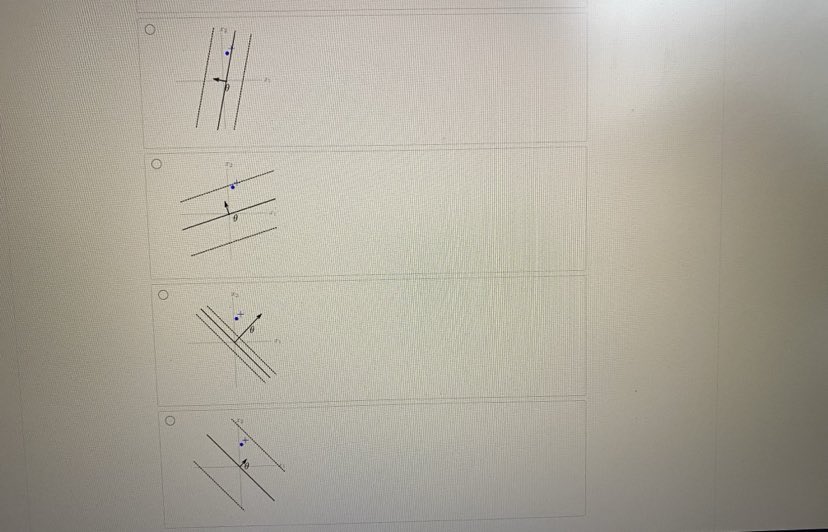
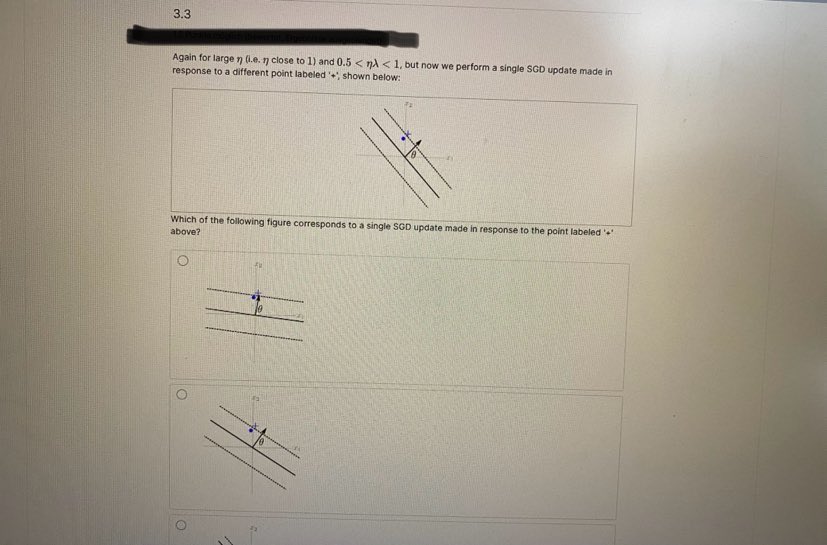
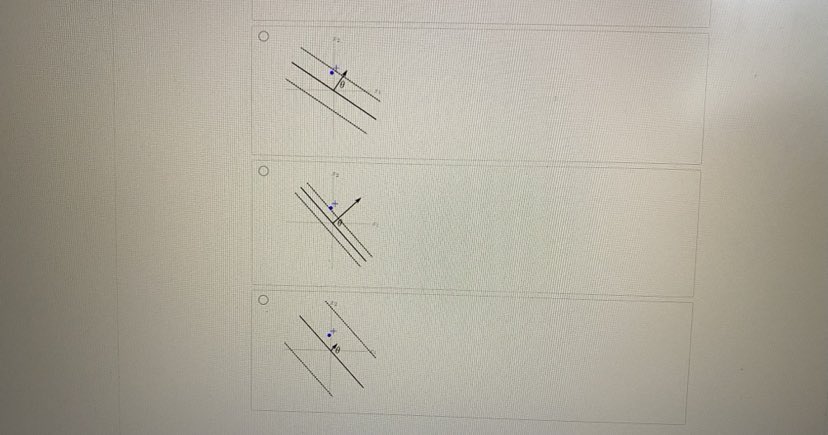
Problem 3 A Bookmark this page Stochastic gradient descent (SGD) is a simple but widely applicable optimization technique. For example, we can use it to train a Support Vector Machine. The objective function in this case is given by: J (0) Lossh (1 00-2() + 1012 where Lossh (z) - max {0, 1 - z} is the hinge loss function, (x(), y ?) ) with for i = 1, ...n are the training examples, with y"") ( {1, -1} being the label for the vector a("). For simplicity, we ignore the offset parameter Go in all problems on this page. 3.1Stochastic gradient descent (SGD) is a simple but widely applicable optimization technique. For example, we can use it to train a Support Vector Machine. The objective function in this case is given by: where Loss, (z) = max {0, 1 - 2} is the hinge loss function, (a(), yl!) ) with for i = 1, .. . n are the training examples, with y." 6 {1, -1} being the label for the vector z"). For simplicity, we ignore the offset parameter 6% in all problems on this page. 3.1 The stochastic gradient update rule Involves the gradient V,Loss, (D()8 . 2) of Loss, (y(20 . 2(") with respect to e Hint Recall that for a k-dimensional vector # = [61 8, .-. @: ] . the gradient of f (6) war.t. 0 is Vof(0) = 24 ... Find V, Loss, (ye - I) in terms of I. (Enter lambda for A, y for y and x for the vector I. Use * for multiplication between scalars and vectors, or for dot products between vectors. Use e for the zero vector. ] For yo . 1 5 1: For yo . = > 1: VoLossa (ye . =) =For 10 . I > 1: = (x . (fi) VSSOTA Let / be the current parameters. What is the stochastic gradient update rule, where 1) > 0 is the learning rate? (Choose all that apply.) 8+ 0- nVe[Lossn (y( )0 - z(0)] - n10 for random z() with label y! !) 6+ 7V. [Loss, (/(08 . x())| + nVe| |8 for random # " with label -V. Losss (y()0 - z(0)] nVo -10| |for random I'll with label y! 0 - 1 - 2 1 \\ Vo Loss, (9 8. z )] nve zel'3.2 Suppose the current parameter 6 is as in the figure below: Here, & is in the direction of the arrow, the solid line represents the classifer defined by 8, and the dotted lines represent the positive and negative margin boundaries. For large i (Le. r close to 1) 0.5