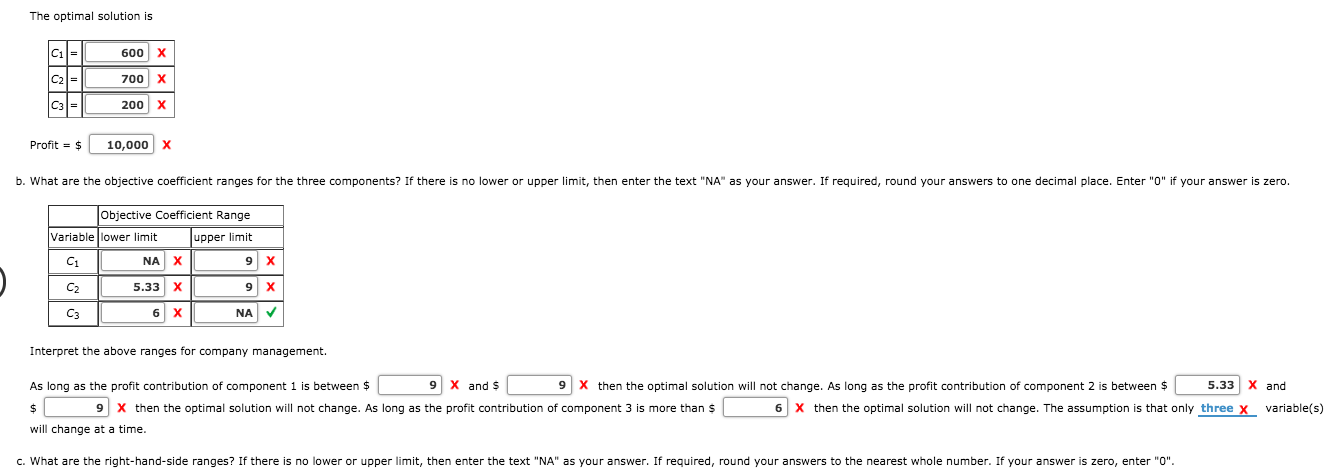
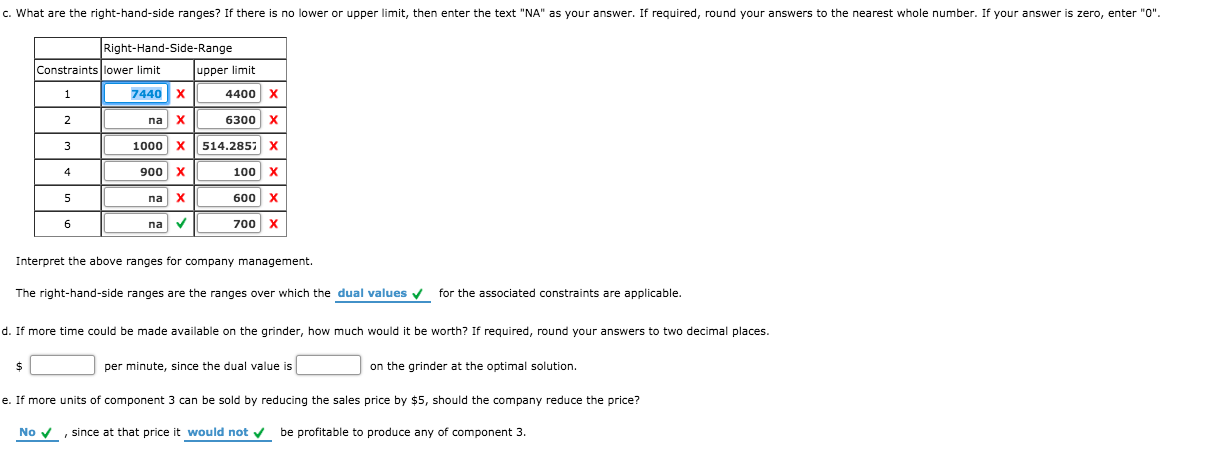
Problem 3-23 (Algorithmic) Vollmer Manufacturing makes three components for sale to refrigeration companies. The components are processed on two machines: a shaper and a grinder. The times in minutes) required on each machine are as follows: Machine Component Shaper Grinder The shaper is available for 130 hours, and the grinder is available for 85 hours. No more than 350 units of component 3 can be sold, but up to 1050 units of each of the other components can be sold. In fact, the company already has orders for 600 units of component 1 that must be satisfied. The profit contributions for components 1, 2, and 3 are $6, $7, and $8, respectively. a. Formulate and solve for the recommended production quantities. If the constant is "1" it must be entered in the box. Let C1 = units of component i manufactured C2 = units of component 2 manufactured C3 = units of component 3 manufactured Max st 16 : 60+ L1 V2+ 5 C2+ 4 + 5 C2 + 1203 5 3 7 ,200 x 6,600 X 200 x 600 x 700 x 200 x constraint 1 Constraint 2 Constraint 3 Constraint 4 Constraint 5 Constraint 6 2 X C1 XC VI 1 IV C1,C2,C3 2 0 The optimal solution is C2= 600 x 700 x 200 x Profit = $ 10,000 b. What are the objective coefficient ranges for the three components? If there is no lower or upper limit, then enter the text "NA" as your answer. If required, round your answers to one decimal place. Enter "0" if your answer is zero. Objective Coefficient Range Variable lower limit upper limit NA 9 C2 5.33 x x Interpret the above ranges for company management. As long as the profit contribution of component 1 is between $ 9 X and $ 9 9 X X then the optimal sol then the optimal solution will not change. As long as the profit contribution of component 2 is between $ 5.33 X and 9 X then the optimal solution will not change. As long as the profit contribution of component 3 is more than $ 6 X then the optimal solution will not change. The assumption is that only three x variable(s) will change at a time. c. What are the right-hand-side ranges? If there is no lower or upper limit, then enter the text "NA" as your answer. If required, round your answers to the nearest whole number. If your answer is zero, enter "O". C. What are the right-hand-side ranges? If there is no lower or upper limit, then enter the text "NA" as your answer. If required, round your answers to the nearest whole number. If your answer is zero, enter "O". Right-Hand-Side-Range Constraints lower limit upper limit 7440x 4400 Una x6300 x 1000 x 514.2857 X 900 x 100 x na x 600 x na U 700 x Interpret the above ranges for company management, The right-hand-side ranges are the ranges over which the dual values for the associated constraints are applicable. d. If more time could be made available on the grinder, how much would it be worth? If required, round your answers to two decimal places. $ per minute, since the dual value is on the grinder at the optimal solution. e. If more units of component 3 can be sold by reducing the sales price by $5, should the company reduce the price? No since at that price it would not be profitable to produce any of component 3