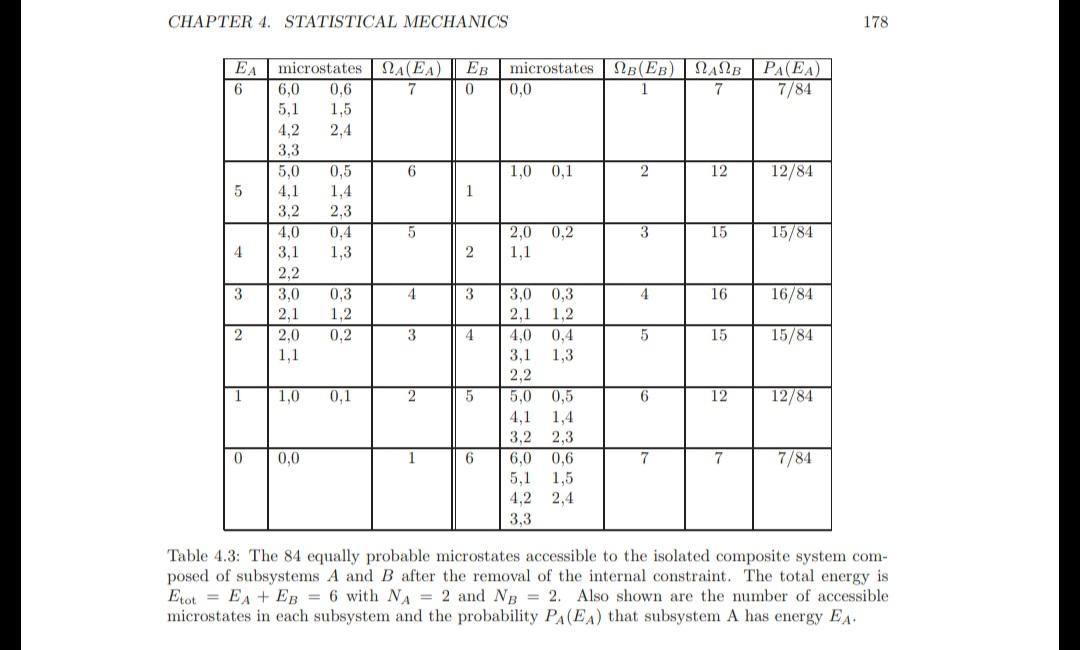
(a) In Table 4.3 we considered a composite Einstein solid of four particles with two particles in each subsystem. Use the results of Table 4.3 to calculate the probability that subsystem A is in a particular microstate. Use EinsteinSolids Program to help answer the following questions. (b) The program computes the probability PA(EA) that subsystem A has energy EA. Consider NA = 4, NB = 12 and Etot = 3. Run the program and collect the data from the Data Table under the Views menu. (c) Determine the probability P:(Es) that subsystem A is in a particular microstate by dividing PA(EA) by the number of microstates with energy EA. Plot P(Es). (d) Explain why the probabilities P, and PA(EA) are not the same. Why is the probability P3(Es) a monotonically decreasing function of E,? What is the qualitative behavior of PA(EA)? CHAPTER 4. STATISTICAL MECHANICS 178 microstates NB(EB) NANB PA(EA) 7/84 EA microstates NA(EA) 6. 6,0 0,6 0,0 1 5,1 1,5 2,4 4,2 3,3 5,0 0,5 6 1,0 0,1 12 12/84 4,1 1,4 1 3,2 2,3 4,0 0,4 2,0 0,2 3 15 15/84 4. 3,1 1,3 1,1 2,2 3 3,0 16/84 0,3 1,2 3 3,0 0,3 4 16 2,1 2,1 1,2 2,0 0.2 3 4. 4,0 0,4 5 15 15/84 1,1 3,1 1,3 2,2 1,0 0,1 2 5,0 0,5 12 12/84 4,1 1,4 3,2 2,3 0,0 1 6,0 0,6 7 7/84 5,1 4,2 1,5 2,4 3,3 Table 4.3: The 84 equally probable microstates accessible to the isolated composite system com- posed of subsystems A and B after the removal of the internal constraint. The total energy is Etot = EA + EB = 6 with NA = 2 and NB = 2. Also shown are the number of accessible microstates in each subsystem and the probability PA(EA) that subsystem A has energy EA.