Question: Problem 5. (12 marks) Connectivity in undirected graphs vs. directed graphs. a. (8 marks) Prove that in any connected undirected graph G = (V,E) with

Problem 5. (12 marks) Connectivity in undirected graphs vs. directed graphs.

a. (8 marks) Prove that in any connected undirected graph G = (V,E) with Problem 5. (12 marks) Connectivity in undirected graphs vs. directed graphs. a. , there are at least two vertices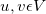 whose removal (along with all the edges that touch them) leaves G still connected. Propose an efficient algorithm to find two such vertices. (Hint: The algorithm should be based on the proof or the proof should be based on the algorithm.)

b. (4 marks) Give an example of a strongly connected directed graph G = (V,E) such that for every 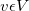with , there are at least two vertices whose removal (along with , removing v (along with all the edges that touches v) from G leaves a directed graph that is not strongly connected.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Problem 5. (12 marks) Connectivity in undirected graphs vs. directed graphs a. (8 marks) Prove that in any connected undirected graph G = (V,E) with Ivi > 2, there are at least two vertices u, v V...

4. (20 points) Connectivity in undirected graphs vs. directed graphs (a) (10 points) Prove that in any connected undirected graph G (V, E) with |VI> 2, there are at least two vertices u, v E V whose...

Problem 5: [4 marks]| Add the following elements to an initially empty B-tree. The order of the B-tree is 8. Draw the resulting B-tree. 33453886532 1121732552367 153911 1948 Problem 6: [4 marks] Show...

Describe an algorithm to generate G2 from G1. [12 marks] How could this algorithm be used to generate the transitive closure of a graph given its adjacency matrix? [5 marks] What is the cost of this...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Hello! Please answer Problem 2, and include any necessary classes from the previous question if they are needed. Thank you! Problem statement A Graph is formally define as G-N,E) consisting of the...

The British developed the jury, and voir dire, but over the past several decades, they have nearly eliminated both. In Britain, there are no juries in any civil case except one of libel or police...

Let X be a normally distributed random variable with mean 410 and standard deviation 2. Find the probability that X will be between 407 and 415.

6. Find an acute angle whose sine is (a) 0.52, (c) 0.875, (b) 0.75, (d) 0.3456.

Identify any energy infrastructure in Ghana or in your Country and clearly evaluate how such infrastructure was financed

4. What kinds of businesses are most likely to benefit from using cloud computing? Why? Cloud computing is taking off. The biggest players in the cloud computing marketplace include Amazon Web...

5-10 Qantas Airways, Australias leading airline, faces cost pressures from high fuel prices and lower levels of global airline traffic. To remain competitive, the airline must find ways to keep costs...

5-13 In MyMISLab, you will find a Collaboration and Teamwork Project dealing with the concepts in this chapter. You will be able to use Google Drive, Google Docs, Google Sites, Google+, or other...