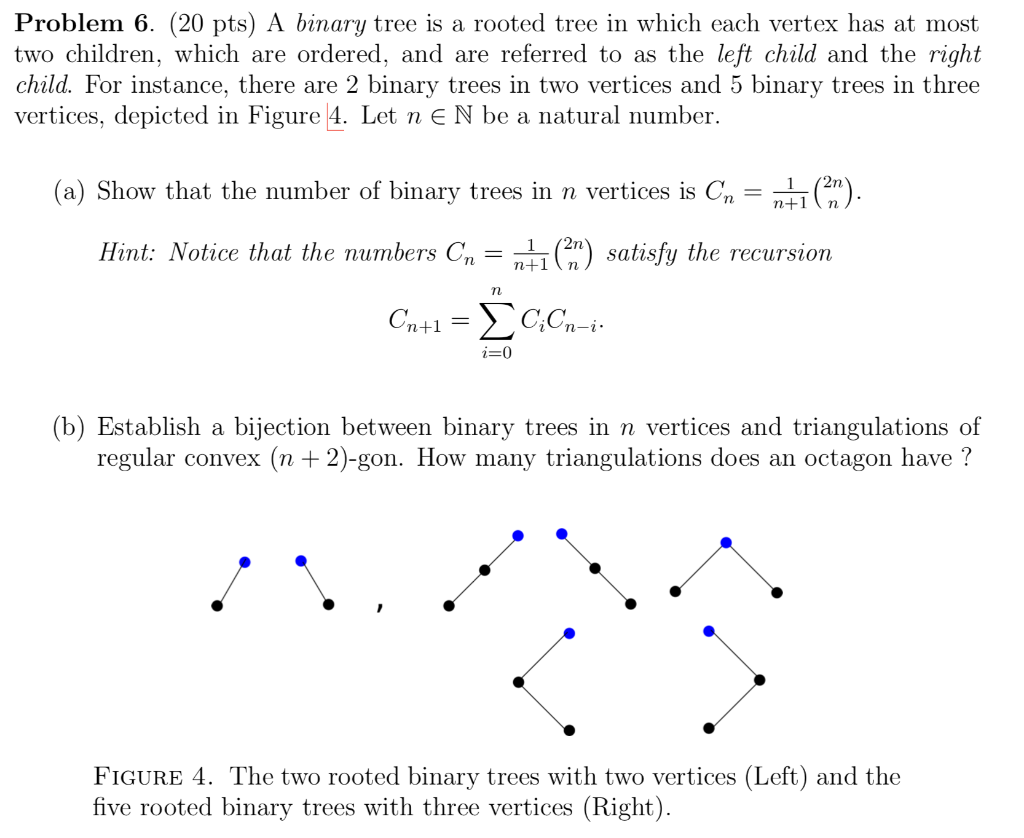
Problem 6. (20 pts) A binary tree is a rooted tree in which each vertex has at most two children, which are ordered, and are referred to as the left child and the right child. For instance, there are 2 binary trees in two vertices and 5 binary trees in three vertices, depicted in Figure 4. Let n EN be a natural number. (a) Show that the number of binary trees in n vertices is Cn n Hint: Notice that the numbers C,-11(2n) satisfy the recursion 1 (2n (b) Establish a bijection between binary trees in n vertices and triangulations of regular convex (n + 2)-gon. How many triangulations does an octagon have? FIGURE 4. The two rooted binary trees with two vertices (Left) and the five rooted binary trees with three vertices (Right) Problem 6. (20 pts) A binary tree is a rooted tree in which each vertex has at most two children, which are ordered, and are referred to as the left child and the right child. For instance, there are 2 binary trees in two vertices and 5 binary trees in three vertices, depicted in Figure 4. Let n EN be a natural number. (a) Show that the number of binary trees in n vertices is Cn n Hint: Notice that the numbers C,-11(2n) satisfy the recursion 1 (2n (b) Establish a bijection between binary trees in n vertices and triangulations of regular convex (n + 2)-gon. How many triangulations does an octagon have? FIGURE 4. The two rooted binary trees with two vertices (Left) and the five rooted binary trees with three vertices (Right)