Question: Problem 6. Suppose that R = ( R , + , * ) is a commutative ring , and let'S be a proper ideal of

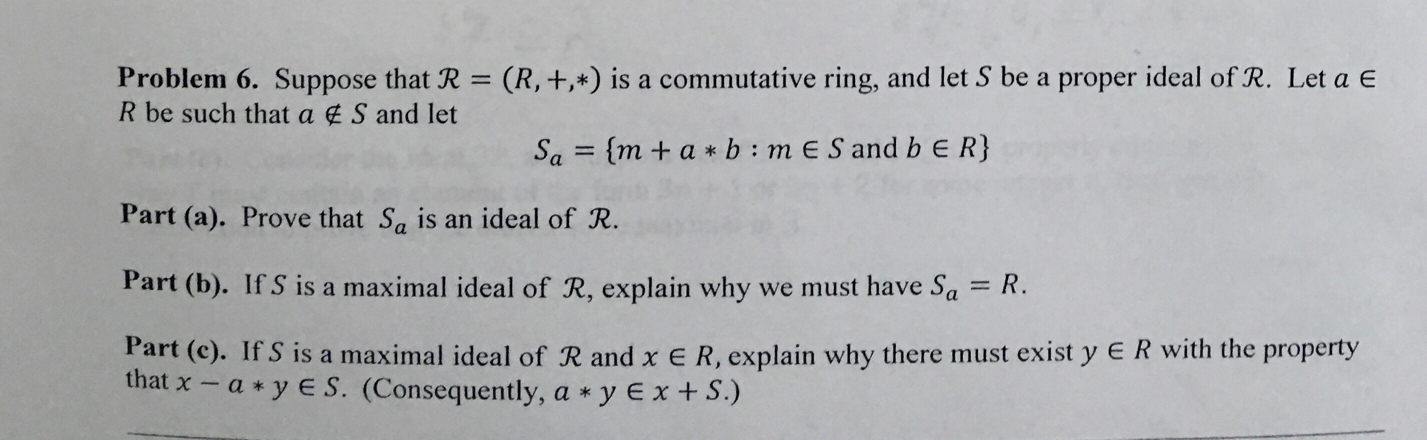
Problem 6. Suppose that R = ( R , + , * ) is a commutative ring , and let'S be a proper ideal of R. Let a E R be such that a ES and let Sa = [ m + a * 6 : ME S and b ER ) Part ( a ) . Prove that Sa is an ideal of R . Part ( b ) . If's is a maximal ideal of R, explain why we must have Sa = R. Part ( C ) . If'S is a maximal ideal of & and * ER, explain why there must exist Y ER with the property that x - a * YES. ( Consequently, a* V E x + 5. )

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let R and S be unital rings, with identity elements 1 and 1s respectively. Suppose that : R S is a possibly-nonunital ring homomorphism. (a) Show that if is nonunital, then (1) is a zero-divisor of...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

1. Consider the two points x 1 = (1, 1), x 2 = (1, 0) in R2 . Draw the set of points which can be obtained by using the following operations. (a) x = 1x 1 + 2x 2 , 1, 2 R (linear combination) (b) x =...

Problem 1: A baseball catcher is performing a stunt for a television commercial. He will catch a baseball with mass mm = I .73 g, dropped from rest at a height yy = 24'. 6 m above his glove. The...

Problem 1. Assume that a is any scalar, and that A, B, and C are matrices of sizes such that the indicated matrix products are defined. Prove the following:1 (i) (associativity) A(BC) = (AB)C. (ii)...

Can you solve as many questions as possible with clear solutions. (I know the second page is blur, even if I tried to fix, although it is readable) 5. The Hatfields, Montagues, McCoys, and Capulets...

Problem 2. Consider the ring 3. Part (a). If a is a prime number, use Euclid's Lemma to show that I (a) is a prime ideal of 3. (See Investigation 18 Problem 8 and Investigation 20 Homework Problem...

Give a one- or two-sentence synopsis of "if' part of Theorem 27.9. Data from Theorem 27.9 Let R be a commutative ring with unity. Then M is a maximal ideal of R if and only if R/M is a field. Proof...

Give a one- or two-sentence synopsis of "only if' part of Theorem 27.9. Data from Theorem 27.9 Let R be a commutative ring with unity. Then M is a maximal ideal of R if and only if R/M is a field....

if do - a, + a2 - . . . (-1)*a, is divisible by 11. 33. Show that the number 7, 176,825,942, 116,027,211 is divisible by 9 but not divisible by 11. 34. Show that the number 9,897,654,527,609,805 is...

1. In April 2019, a market view on the FTSE100 index from an analyst was given as below: Probability FTSE100 Return 20% 0.7 0.2 5% 0.1 -30% Scenario Bull Neutral Bear Discuss your market view on the...

The following information was taken from the 2012 annual report of Target Corporation (dollars in millions): a. Compute the inventory purchases made by Target during 2012. Record a single entry that...

an investor is consideting making an offer on a florida property to build a solar fam, What envuitomental issue should the investor contemplate before purchasin g the property

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...