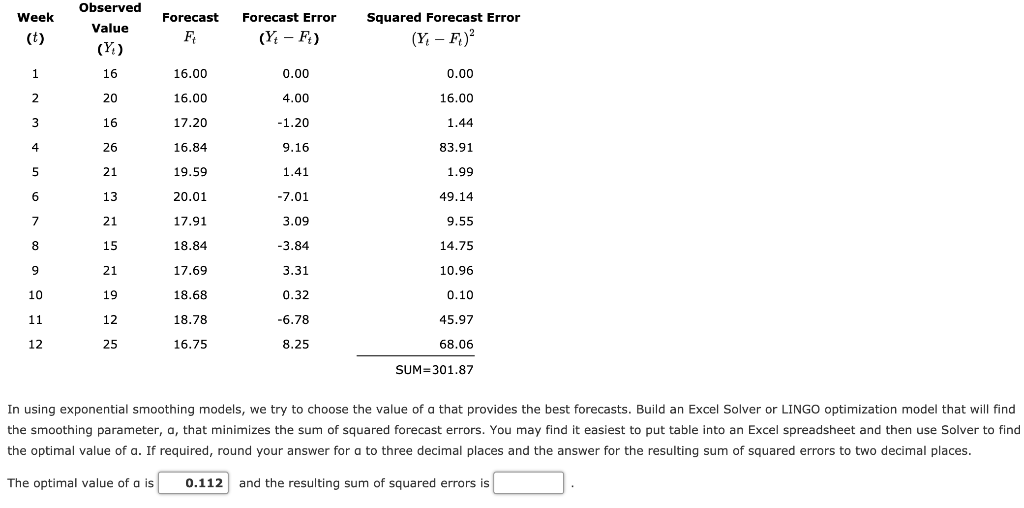
Question: Problem 8-12 (Algorithmic) Many forecasting models use parameters that are estimated using nonlinear optimization. The basic exponential smoothing model for forecasting sales is Ft +

Problem 8-12 (Algorithmic) Many forecasting

Problem 8-12 (Algorithmic) Many forecasting models use parameters that are estimated using nonlinear optimization. The basic exponential smoothing model for forecasting sales is Ft + 1 = aYt + (1 - a)Ft where Ft + 1 = forecast of sales for period t + 1 Yt = actual value of sales for period t Ft = forecast of sales for period t a = smoothing constant osasi This model is used recursively; the forecast for time period t + 1 is based on the forecast for period t, Fe; the observed value of sales in period t, Y and the smoothing parameter a. The use of this model to forecast sales for 12 months is illustrated in the table below with the smoothing constant a = 0.3. The forecast errors, Yt - Ft, are calculated in the fourth column. The value of a is often chosen by minimizing the sum of squared forecast errors, commonly referred to as the mean squared error (MSE). The last column of Table shows the square of the forecast error and the sum of squared forecast errors. EXPONENTAL SMOOTHING MODEL FOR Q=0.3 Week Observed Value Forecast F Forecast Error (Y4 - Ft) Squared Forecast Error (Y4 - F)? 16 16.00 0.00 0.00 1 2 20 16.00 4.00 16.00 3 16 17.20 -1.20 1.44 4 26 16.84 9.16 83.91 Week (t) Observed Value (Y) Forecast F Forecast Error (Y - Ft) Squared Forecast Error (Y - F) 1 16 16.00 0.00 0.00 2 20 16.00 4.00 16.00 3 16 17.20 -1.20 1.44 4 26 16.84 9.16 83.91 5 21 19.59 1.41 1.99 6 13 20.01 -7.01 49.14 7 21 17.91 3.09 9.55 8 15 18.84 -3.84 14.75 9 21 17.69 3.31 10.96 10 19 18.68 0.32 0.10 11 12 18.78 -6.78 45.97 12 25 16.75 8.25 68.06 SUM=301.87 In using exponential smoothing models, we try to choose the value of a that provides the best forecasts. Build an Excel Solver or LINGO optimization model that will find the smoothing parameter, a, that minimizes the sum of squared forecast errors. You may find it easiest to put table into an Excel spreadsheet and then use Solver to find the optimal value of a. If required, round your answer for a to three decimal places and the answer for the resulting sum of squared errors to two decimal places. The optimal value of a is 0.112 and the resulting sum of squared errors is

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

Many forecasting models use parameters that are estimated using nonlinear optimization. The basic exponential smoothing model for forecasting sales is Ft + 1 = aYt + (1 - a) Ft where Ft + 1 =...

Many forecasting models use parameters that are estimated using nonlinear optimization. The basic exponential smoothing model for forecasting sales is F t + 1 = Y t + (1 ) F t where F t + 1 =...

Many forecasting models use parameters that are estimated using nonlinear optimization. The basic exponential smoothing model for forecasting sales is F+ -a + (1 - 0) where F+ - forecast of sales for...

Many forecasting models use parameters that are estimated using nonlinear optimization. A good example is the Bass model introduced in this chapter. Another example is the exponential smoothing...

Many forecasting models use parameters that are estimated using nonlinear optimization. This is true of many of the models developed in Chapter 6. Consider the exponential smoothing forecasting model...

Many forecasting models use parameters that are estimated using nonlinear optimization. A good example is the Bass model introduced in this chapter. Another example is the exponential smoothing...

Many forecasting models use parameters that are estimated using nonlinear optimization. A good example i s the Bass model introduced i n this chapter. Another example i s the e x - ponential...

Many forecasting models use parameters that are estimated using nonlinear optimization. A good example is the Bass model introduced in this chapter. Another example is the exponential smoothing...

The inventory system is periodic, and the cost method is FIFO. Beginning inventory is $2,600 million (100 million units). (The beginning balance of inventory in the trial balance includes this amount...

Refer to Exhibit. For each risk assessment principle, provide

Which of the foliowing best destribes the effect of a contingent fee arrangerment on the zosvors independence? The cemtineent lye arrangement does met impar independence umless more than half of the...

As the manager of Smith Construction, you need to make a decision on the number of homes to build in a new residential area where you are the only builder. Unfortunately, you must build the homes...