problem2Find a function V(x) that gives the volume of water in the through if the height of the water is x metersproblem 3find the linearization of the volume function you found in problem 2 based at x=1.5 metersproblem 4use the linearization in problem 3 to estimate the change in volume of water in the through if we increase the height in water in the tank by 0.1 metersproblem 5repeat the instructions given in problem 3 this time base the linearization at x=2.5 metersproblem 6use the linearization from problem 5 to estimate the change in volume of water in the through if we increase the height of water in the tank by 0.4 metersproblem 7compare the result in problem 4 to the following evaluation deltaV=V(1.6)-V(1.5)Compare the result in problem 6 to the following evaluation deltaV=V(2.9)-V(2.5)what did you notice?problem 8 The linearization of f(x) at x=a is found via the following sequence of related approximationsf'(a)?{f(x)-f(a)}/x-af(x) - f(a) ? f'(a)(x-a)f(x) ? f(a) + f'(a)(x-a)a) where does the initial approximation stem fromb)give the formula for L(x) (the linearization of f(x) based at x?a)Problem 9Recall thatf'(a) = df/dxThen, the initial approximation given in problem 8 can be re-expressed as f'(a)= df/dx ? {f(x)-f(a)}/x-a = delta f/ delta xdefine: dx=delta x Also define: df=f'(a)dxThen Delta f?dfsynthesize this result with your observations in problem 7

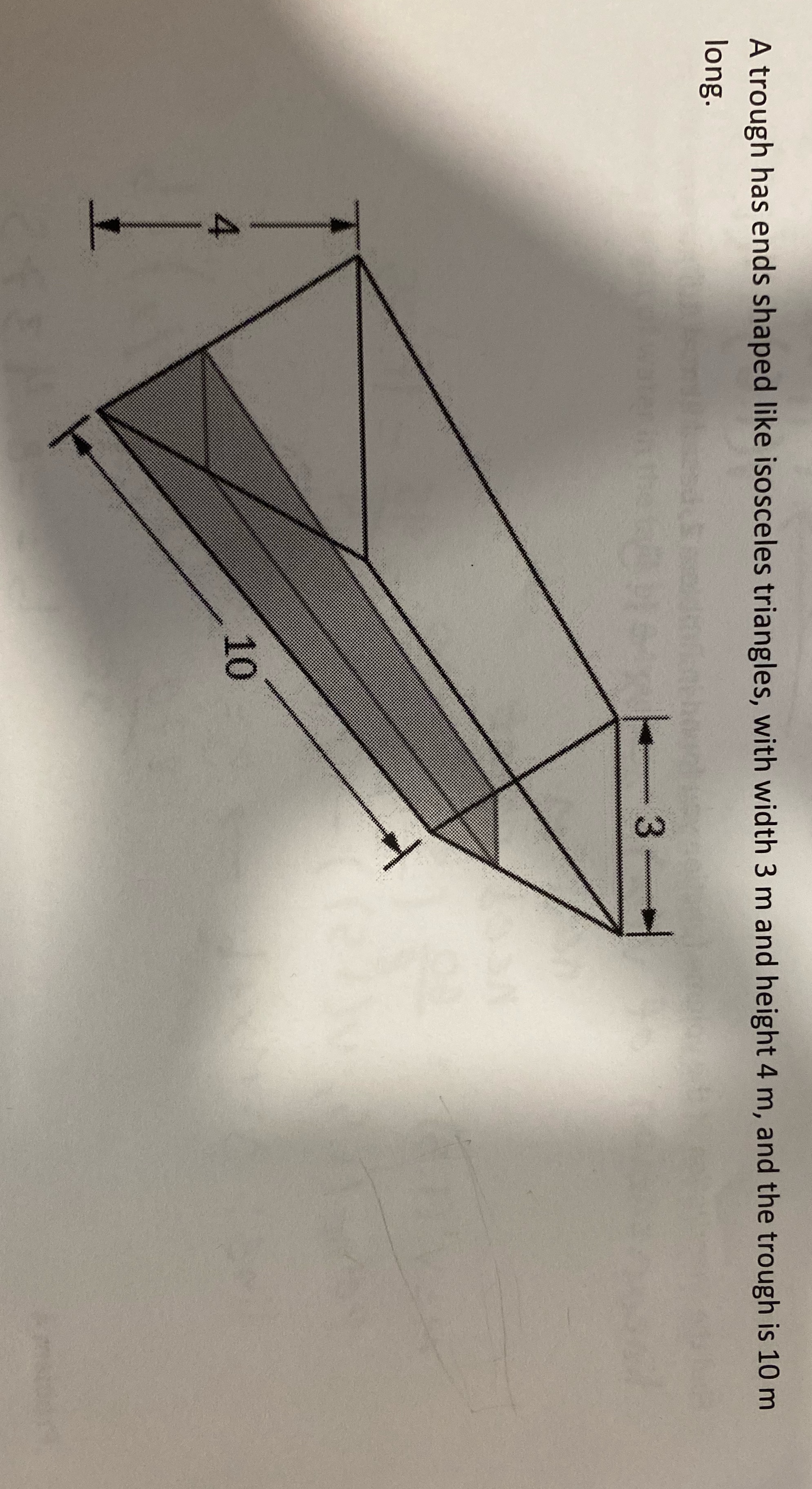
A trough has ends shaped like isosceles triangles, with width 3 m and height 4 m, and the trough is 10 m long