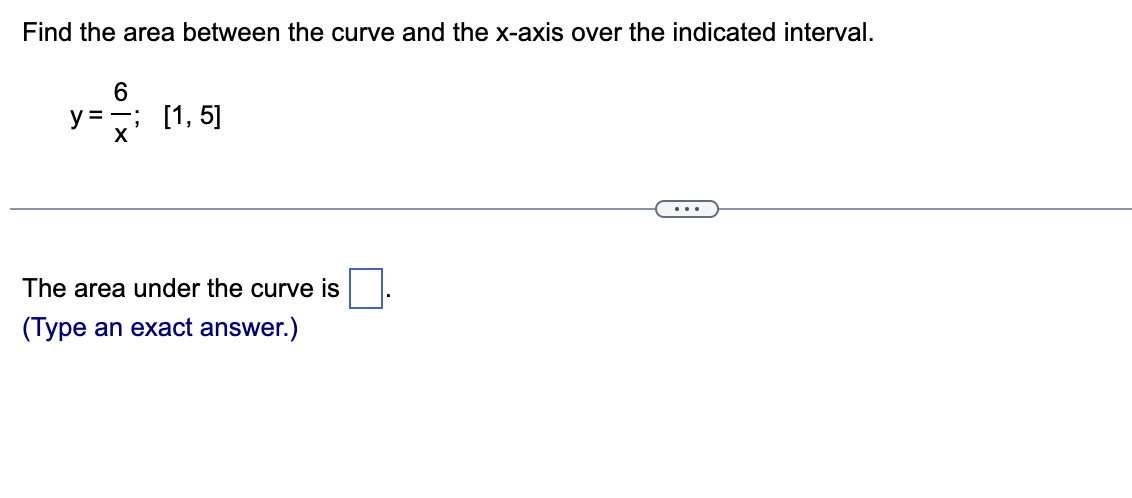
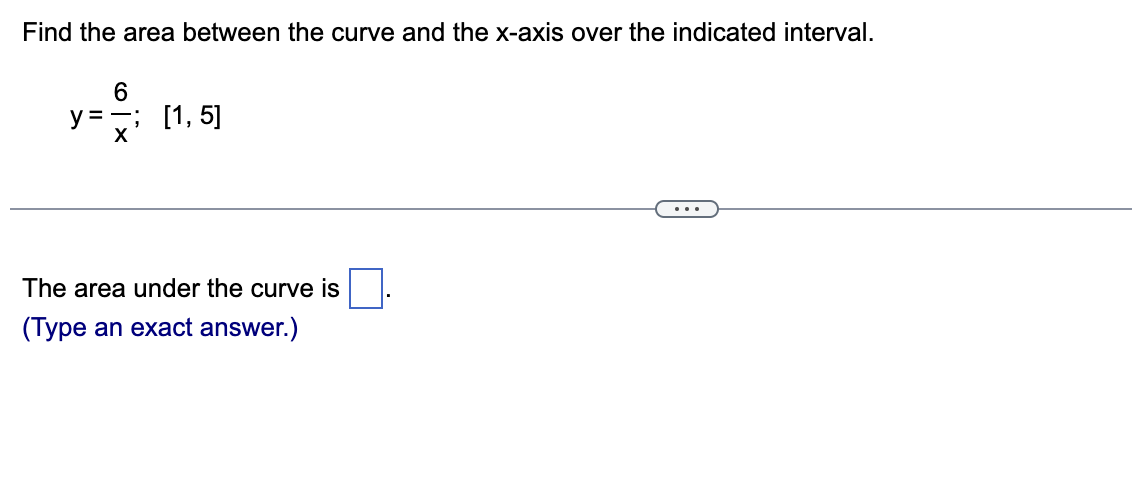
Prove that secx dx = In /secx+ tan x| + C. (Hint: Multiply the numerator and denominator of the integrand by sec x + tan x; then make a change of variables u = sec x + tan x.) Evaluate the left side. Start by multiplying the numerator and denominator of the integrand by sec x + tan x. sec x( sec x + tan x) - sec x dx = dx 1( sec x + tan x) dx Multiply. sec x + tan x (Simplify your answer.)Find the area between the curve and the x-axis over the indicated interval. 6 y=;; [1.5] The area under the curve is E. (Type an exact answer.) Evaluate the following integral. It 5 I? 1+ cos 2xdx 0 E It 5 I7 1 + cos 2x dx= E (Type an exact answer, using radicals as needed.) 0 Find the volume of the solid generated when the region bounded by the graph ofy= cosx and the x-axis on the interval [- 21:, 0] is revolved about the xaxis. E} The described volume is El cubic units. (Type an exact answer, using 11: as needed.)