Python 3 help! Looking for coding help! Not help with theory or pseudocode! I understand the math part but am stuck on how to implement it in Python! Using variables it runs great BUT if i try to use set integers I can't get the program to run properly.

The issue is making groups of (i used n as a variable in this example) 3 with at least 1 man per group.

So n=3 (groups of three people)

k= 1 (number of men at a minimum)

m = total number of men

w = total number if women

So if there are 2 men and 2 women our groups will look like this:

m1w1w2

m2w1w2

m1m2w1

m1m2w2

This seems easier when i just throw in variables, but how can i set n=3 and k=1 (min number of men) in the code? I'm just really stuck on this one question to get python to run it in Jupyter! i know theres probably an easy fix, to just have

def ways (w,m) run with set numbers for group size (n =3) and minimum number of men (k=1, 2, 3 depending on variable m).

what would the code look like?

i would like to print the number of combinations of teams of three of men and women with at least one man. im just getting stuck on how to set n=3 and k= at least 1

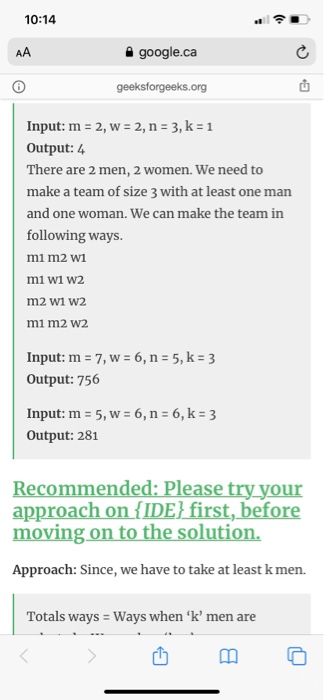
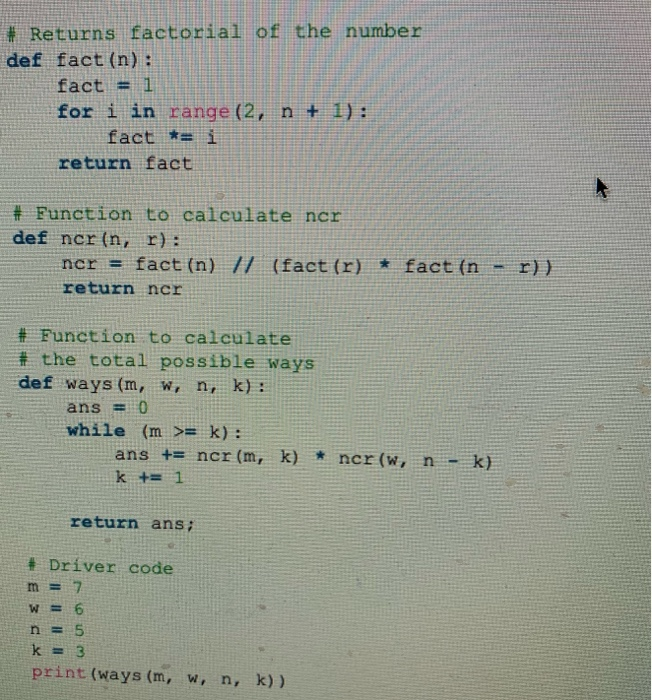
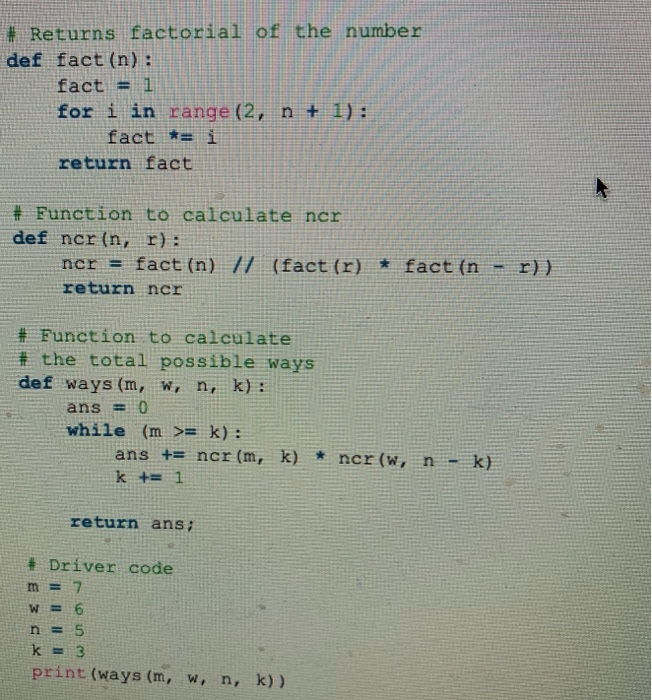
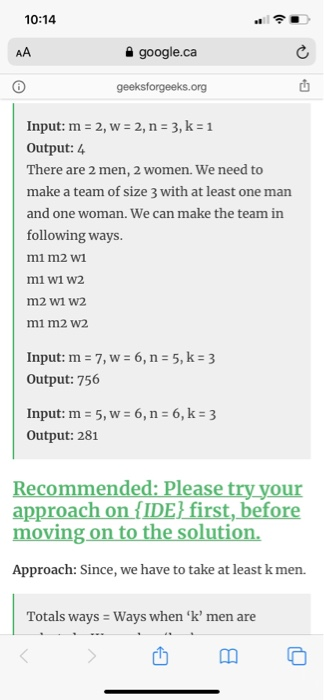
10:14 AA google.ca c geeksforgeeks.org Input: m = 2, w = 2, n = 3, k = 1 Output: 4 There are 2 men, 2 women. We need to make a team of size 3 with at least one man and one woman. We can make the team in following ways. mi m2 w1 mi wi w2 m2 w1 W2 mi m2 w2 Input: m = 7, W = 6, n = 5, k = 3 Output: 756 Input: m = 5, W = 6, n = 6, k = 3 Output: 281 Recommended: Please try your approach on {IDE} first, before moving on to the solution. Approach: Since, we have to take at least k men. Totals ways = Ways when 'k' men are # Returns factorial of the number def fact (n) : fact = 1 for i in range (2, n + fact *= i return fact # Function to calculate ner def ncr in, r): ncr = fact (n) // (fact (r) * fact (n - r)) return ner # Function to calculate # the total possible ways def ways (m, w, n, k): ans = 0 while (m >= k): ans += ner (m, k) * ncr (w, n - k) k += 1 return ans; # Driver code m = 7 6. n = 5 k = 3 print (ways (m, w, n, k)) # Returns factorial of the number def fact (n) : fact = 1 for i in range (2, n + fact *= i return fact # Function to calculate ner def ncr in, r): ncr = fact (n) // (fact (r) * fact (n - r)) return ner # Function to calculate # the total possible ways def ways (m, w, n, k): ans = 0 while (m >= k): ans += ner (m, k) * ncr (w, n - k) k += 1 return ans; # Driver code m = 7 n = 5 k = 3 print (ways (m, w, n, k)) 10:14 AA google.ca c geeksforgeeks.org Input: m = 2, w = 2, n = 3, k = 1 Output: 4 There are 2 men, 2 women. We need to make a team of size 3 with at least one man and one woman. We can make the team in following ways. mi m2 w1 mi wi w2 m2 w1 W2 mi m2 w2 Input: m = 7, W = 6, n = 5, k = 3 Output: 756 Input: m = 5, W = 6, n = 6, k = 3 Output: 281 Recommended: Please try your approach on {IDE} first, before moving on to the solution. Approach: Since, we have to take at least k men. Totals ways = Ways when 'k' men are