python code for all commented parts please

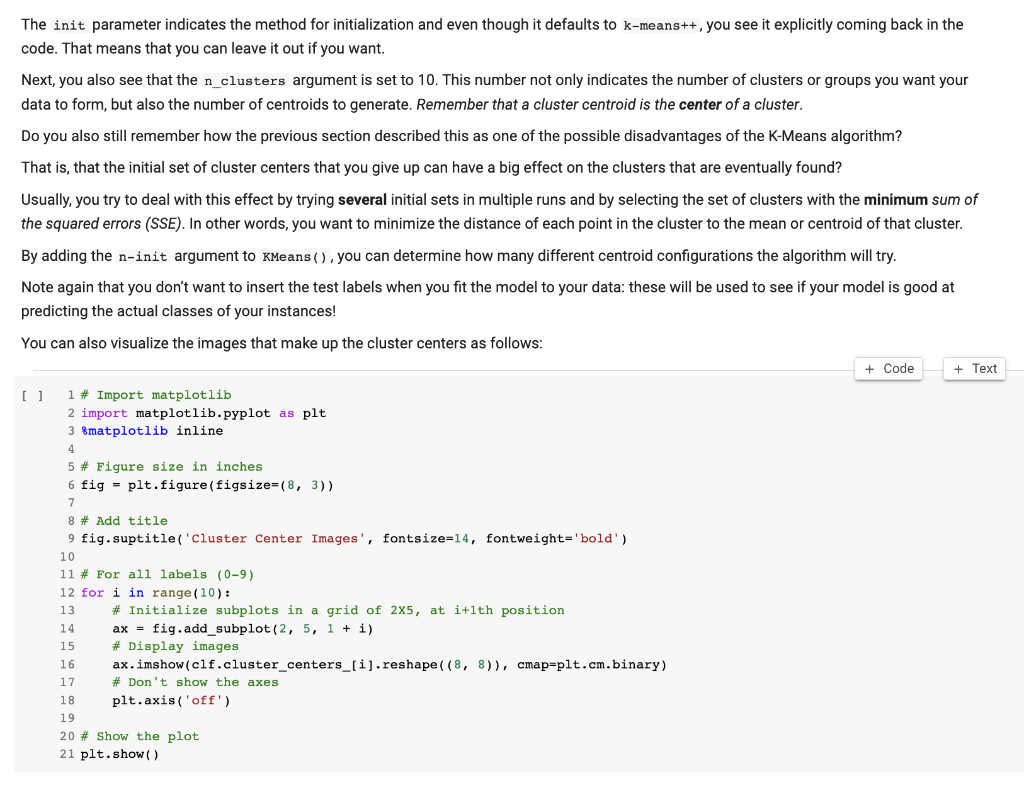
Now, it's finally time to find those clusters of your training set. Use KMeans() from the cluster module to set up your model. You'll see that there are three arguments that are passed to this method: init, n_clusters and the random_state. You might still remember this last argument from before when you split the data into training and test sets. This argument basically guaranteed that you got reproducible results. Please use the same random_state here. The other important thing here is determining the value of k in n clusters. Here it is easy ( n clusters =10 ) since we already know that the data has 10 classes. There is a greater chance we you conduct an unsupervised learning analysis and you do not have classes - then you will have to try different value of k. 1 \# Import the 'cluster' module 2 3 4 \# Create the KMeans model 5 clf = cluster.KMeans(init='k-means++', n_clusters=10, random_state=2019) 6 7 \# Fit the training data 'x_train'to the model 8 The init parameter indicates the method for initialization and even though it defaults to k-means++, you see it explicitly coming back in the code. That means that you can leave it out if you want. Next, you also see that the n_clusters argument is set to 10 . This number not only indicates the number of clusters or groups you want your data to form, but also the number of centroids to generate. Remember that a cluster centroid is the center of a cluster. Do you also still remember how the previous section described this as one of the possible disadvantages of the K-Means algorithm? That is, that the initial set of cluster centers that you give up can have a big effect on the clusters that are eventually found? Usually, you try to deal with this effect by trying several initial sets in multiple runs and by selecting the set of clusters with the minimum sum of the squared errors (SSE). In other words, you want to minimize the distance of each point in the cluster to the mean or centroid of that cluster. By adding the n-init argument to KMeans ( ), you can determine how many different centroid configurations the algorithm will try. Note again that you don't want to insert the test labels when you fit the model to your data: these will be used to see if your model is good at predicting the actual classes of your instances! You can also visualize the images that make up the cluster centers as follows