python

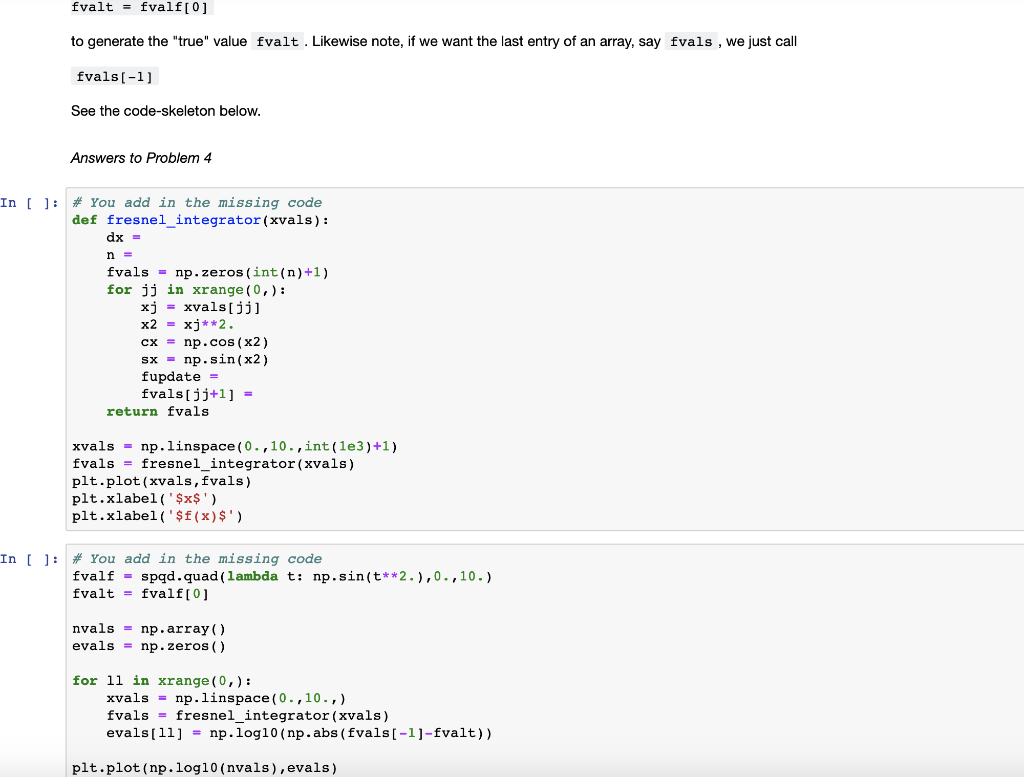
import numpy as np import matplotlib.pyplot as plt import scipy.integrate as spqd &matplotlib inline def fib_general (n,a,s0,s1): #add code here return pn "Problem 4* Let the Fresnel function f(x) be defined via the integral sin(t')dt 4a) (2pts) Write the code that creates a sequence of n + 1 points x,j such that 0 S x, S x, with Fl 4b) (2pts) Find the second order Taylor polynomial approximation around Xj of sin(p), i.e. find T2(t; xj) 4c) (2pts) Using the fact that ox = xj+1-Xj, show that j+1 xj Note, the u-substitution u-xj will make your life so much easier here 4d) (4pts) Using basic properties of integrals and Taylor series, show that xj+1 f(xm) =f(x) + sin(t-)dt *j *j+1 Using the code-skeleton below, write a Python function called fresnel_integrator which takes an array xvals and returns a corresponding array fvals , which contains the values of the Fresnel function f(x). Plot f(x) for 0