python please

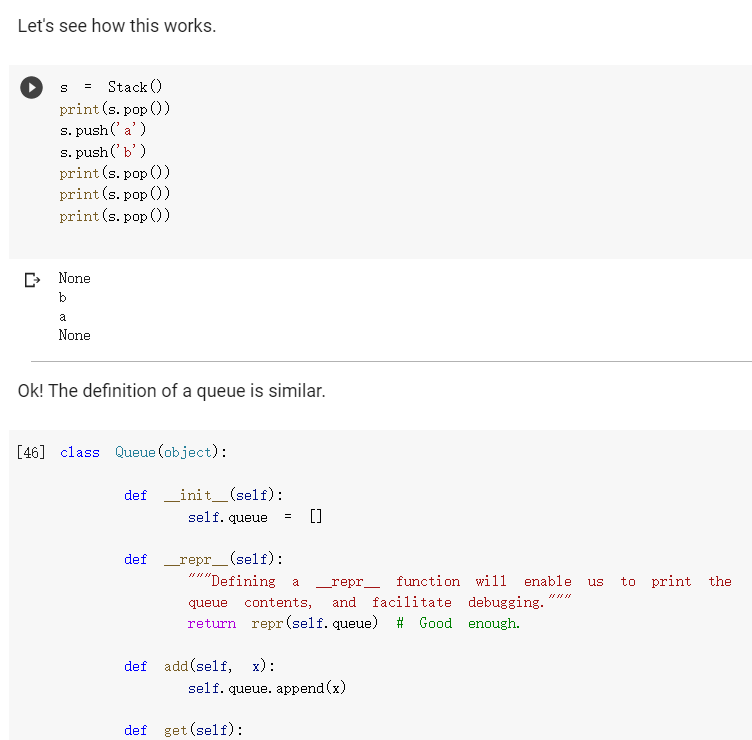
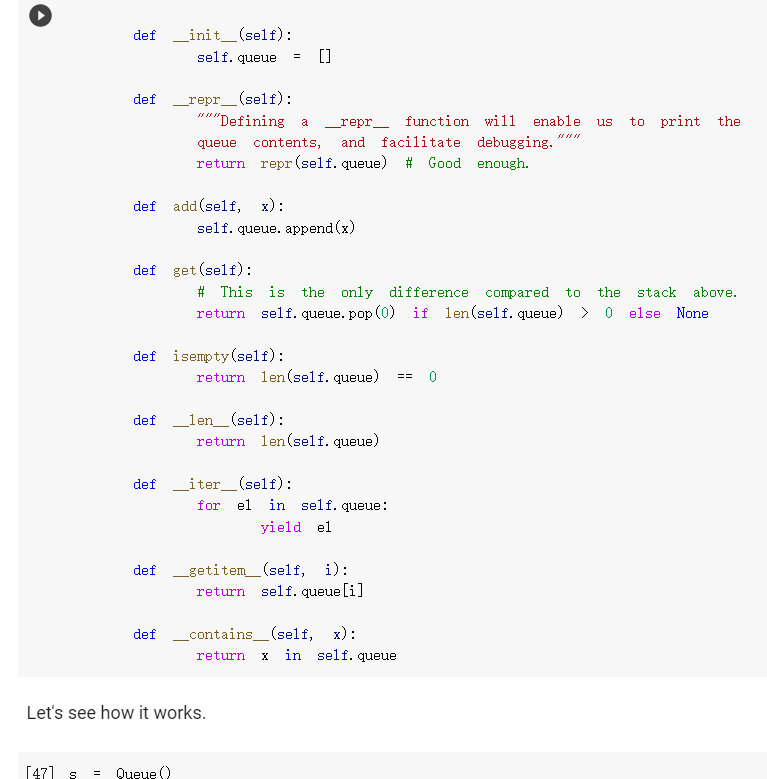
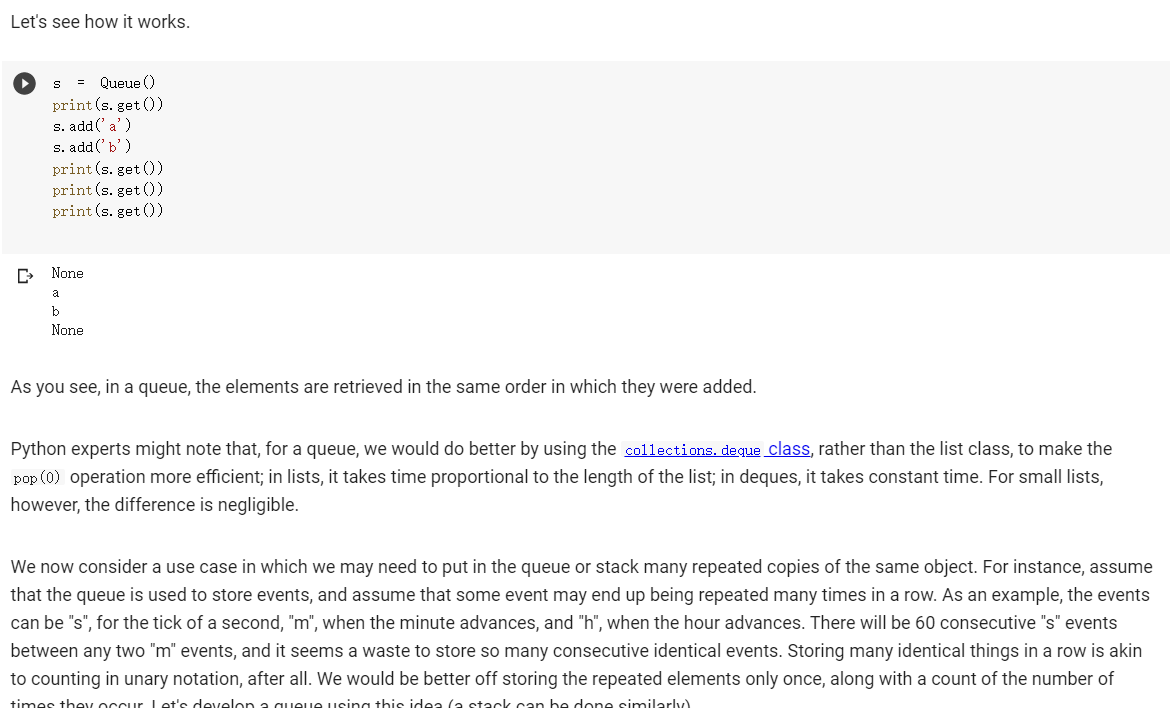
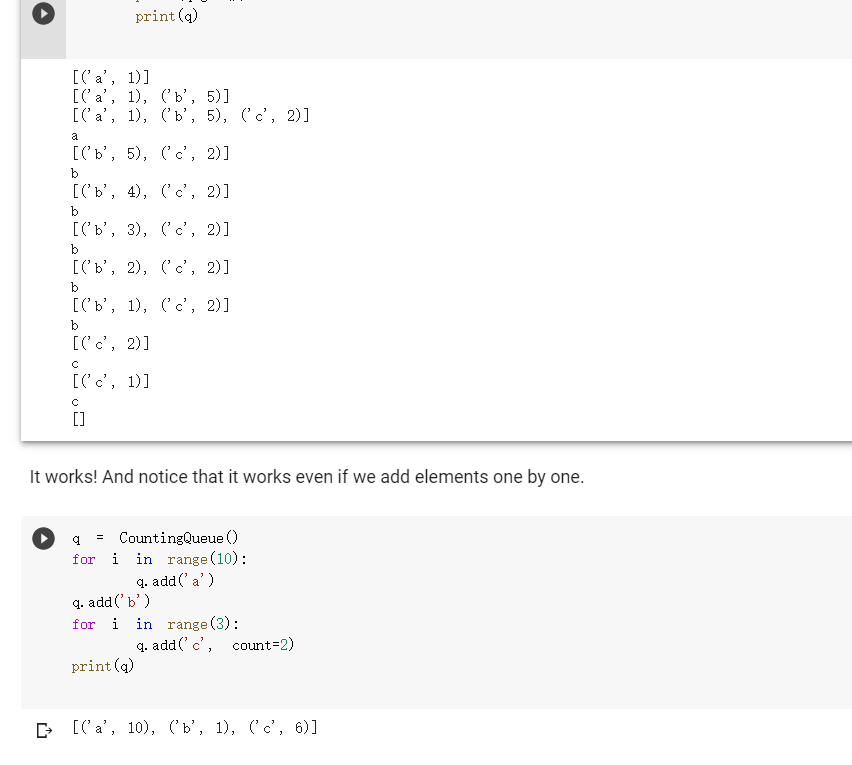
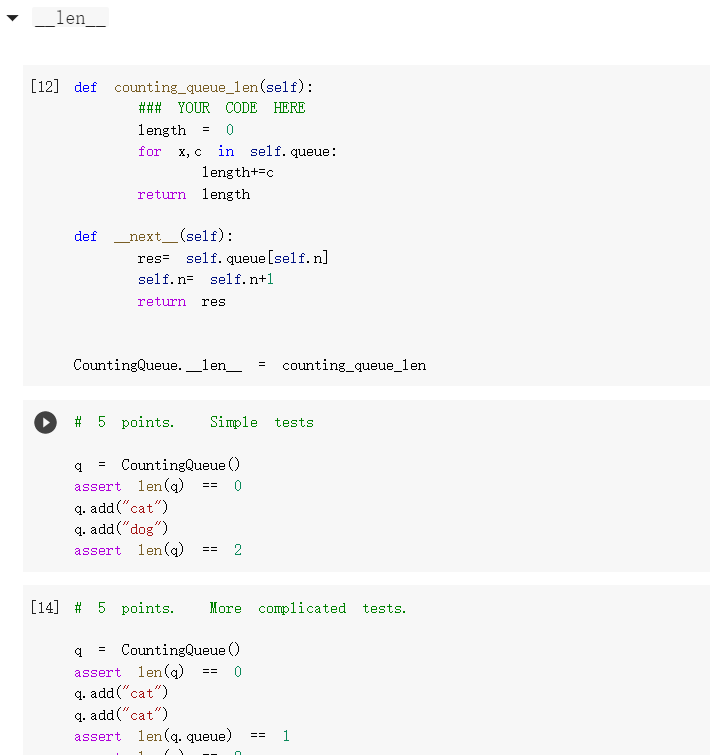
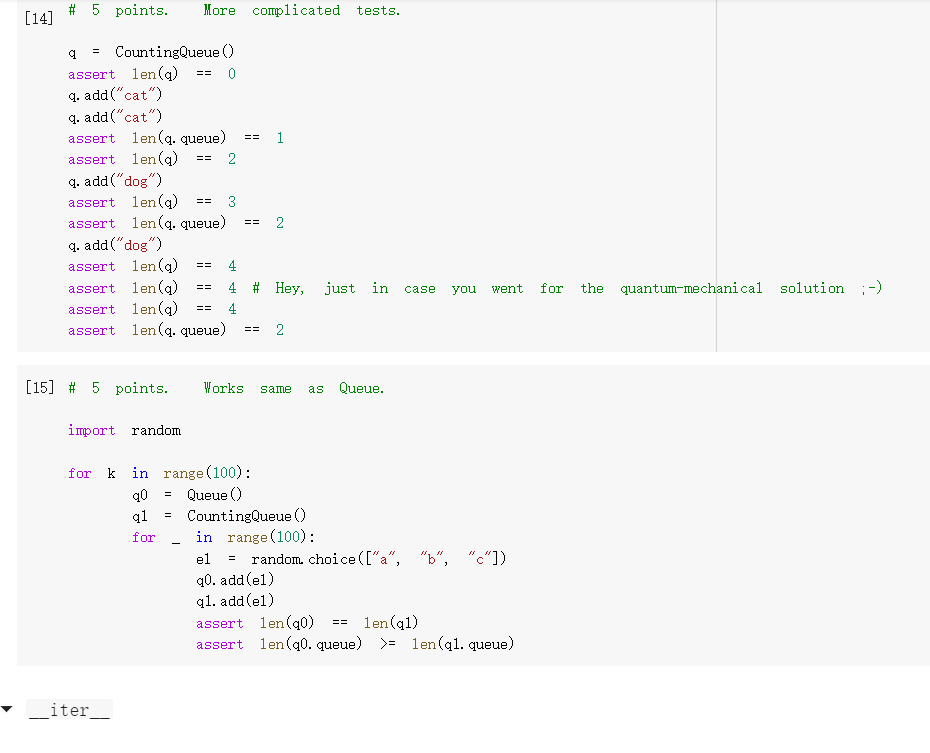
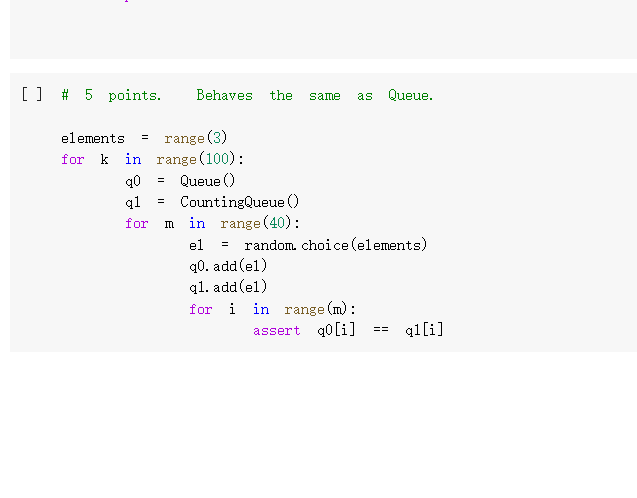
class Stack(object): def _init__(self): self. stack [] def a us to print the repr__(self): "Defining _repr__ function will enable stack contents, and facilitate debugging.' return repr(self. stack) # Good enough. def push(self, **"The "top" of the self. stack. append(x) stack is the end of the list. def pop (self): return self. stack.pop() if len(self. stack) > 0 else None def isempty(self): return len(self. stack) == 0 def _len_(self): return len(self. stack) def Liter_(self): for el in self. stack: yield el def _getitem_(self, i): return self. stack[i] def-contains_(self, x): X in self. stack return Let's see how this works. S = Stack() print (s.pop() s. push('a') S. push('b') print(s.pop()) print (s.pop() print(s.pop()) None b a None Ok! The definition of a queue is similar. [46] class Queue (object): def __init__(self): self. queue [] def _(self): a us to print the repr "Defining _repr__ function will enable queue contents, and facilitate debugging. return repr (self. queue) # Good enough. def x): add(self, self. queue. append(x) def get (self): def __init__(self): = self. queue [] def us to print the repr_(self): ***"Defining a _repr_ function will enable queue contents, and facilitate debugging. return repr(self. queue) # Good enough. def add(self, x): self. queue. append(x) def get (self): # This is the only difference compared to the stack above. return self. queue.pop(0) if len(self. queue) > 0 else None def isempty(self): return len(self. queue) == 0 def _len_(self): len(self. queue) return def Liter__(self): for el in self. queue: yield el def _getitem__(self, i): return self. queue[i] def _contains__(self, x): return x in self. queue Let's see how it works. 47 = Queue () Let's see how it works. S Queue 0 print (s.get) S.add('a') S.add('b') print (s.get) print(s.get()) print (s.get) None a b None As you see, in a queue, the elements are retrieved in the same order in which they were added. Python experts might note that, for a queue, we would do better by using the collections, deque class, rather than the list class, to make the pop (0) operation more efficient; in lists, it takes time proportional to the length of the list; in deques, it takes constant time. For small lists, however, the difference is negligible. We now consider a use case in which we may need to put in the queue or stack many repeated copies of the same object. For instance, assume that the queue is used to store events, and assume that some event may end up being repeated many times in a row. As an example, the events can be "s", for the tick of a second, "m", when the minute advances, and "h", when the hour advances. There will be 60 consecutive "s" events between any two "m" events, and it seems a waste to store so many consecutive identical events. Storing many identical things in a row is akin to counting in unary notation, after all. We would be better off storing the repeated elements only once, along with a count of the number of times they occur let's develona queue using this ideal stack can be done similarly class CountingQueue (object): def __init__(self): self. queue = [] def _repr_(self): return repr(self. queue) same def add(self, count=1): # If the element is the as the last element, we simply # increment the count. This assumes we can test equality of # elements. if len(self. queue) > 0: CC self. queue [-1] if self. queue [-1] (xx, + count) else: self. queue. append((x, count)) else: self. queue [(x, count)] XX = CC == C = C def get (self): if len(self. queue) 0: return None self. queue [0] if 1: self. queue. pop (0) return else: self. queue [0] (x, C - 1) return def isempty(self): [] q CountingQueue () q. add("cat", count=2) q. add("dog" count=3) # Raise IndexError when it's too high... try: q[5] assert False, "Failed to raise IndexError" except IndexError: pass assert q[4] 'dog try: q[5] assert False, "Failed to raise IndexError" except IndexError: pass == # And also when it's too low. try: q[-1] assert False, "Failed to raise IndexError" except IndexError: pass a non-integer. # And raise TypeError if you try to index with try: q["hello"] assert False, "Failed to raise TypeError" except TypeError: pass [] # 5 points. Behaves the same as Queue. elements range (3) print(a) [('a', 1)] [('a', 1), ('b', 5)] [('a', 1), ('b', 5), ('0', 2)] a [('b', 5), ('c', 2)] b [('b', 4), ('0', 2)] b [('b', 3), ('0', 2)] b [('b', 2), ('c', 2)] b [('b', 1), ('0', 2)] b [('c', 2)] C ico , 1 [('c', 1)] [] It works! And notice that it works even if we add elements one by one. q = CountingQueue () for i in range(10): q. add('a') q. add('b') for i in range (3): q. add('c', count=2) print(a) - [('a', 10), ('b', 1), ('d', 6)] _len_ [12] def counting_queue_len(self): ### YOUR CODE HERE length 0 for X,C in self. queue: length+=0 return length def next (self): res= self. queue [self.n] self.n= self.n+1 return res CountingQueue. _len_ counting_queue_len # 5 points. Simple tests q CountingQueue () assert len(q) 0 q. add("cat") q. add("dog") assert len() 2 == [14] # 5 points. More complicated tests. == q CountingQueue) assert len() 0 q. add("cat") q. add("cat") assert len(q. queue) == 1 # 5 points. [14] More complicated tests. = == q CountingQueue () assert len(a) 0 q. add("cat") q. add("cat") assert len(q. queue) 1 assert len(a) 2 q. add("dog") assert len(a) 3 assert len(q. queue) 2 q. add("dog') assert len(a) 4 assert len(a) 4 # Hey, just in assert len(a) 4 assert len(q. queue) 2 == == == case you went for the quantum-mechanical solution ;-) == [15] # 5 points. Works same as Queue. import random for k in range(100): q0 Queue q1 CountingQueue () for in range(100): el random choice (["a", "b", "O"]) qo.add(el) ql.add(el) assert len(0) len(1) assert len(q0. queue) >= len(q1. queue) iter The Homework Assignment For this homework, you must implement the following methods for CountingQueue : _len__ Liter _in_ _getitem_ Your goal is to have CountingQueue behave exactly like Queue to an outside user: the objects have to be different only due to their internal implementation. So for instance, _len_ must return the number of elements, including repetitions; not the number of (element, count) pairs in self. queue. Note that we are adding methods to a class that has already been defined, so our definition have the following somewhat unusual form: == 0: def counting_queue_peek (self): if len(self. queue) return None el, self. queue [0] return el CountingQueue. peek counting_queue_peek In other words, we first create a function (in this case counting_queue_peek ) and then we assign it to the method peek of CountingQueue . It's a bit unusual, but it works, and it relieves us from the task of redefining the class each time we need a new method. [] g = CountingQueue () q. add("cat") q. add("dog") q. peek) [] q CountingQueue () q. add("cat", count=2) q. add("dog" count=3) # Raise IndexError when it's too high... try: q[5] assert False, "Failed to raise IndexError" except IndexError: pass assert q[4] 'dog try: q[5] assert False, "Failed to raise IndexError" except IndexError: pass == # And also when it's too low. try: q[-1] assert False, "Failed to raise IndexError" except IndexError: pass a non-integer. # And raise TypeError if you try to index with try: q["hello"] assert False, "Failed to raise TypeError" except TypeError: pass [] # 5 points. Behaves the same as Queue. elements range (3) [ ] # 5 points. Behaves the same as Queue. range (3) = IIL elements for k in range(100): qo Queue () q1 CountingQueue () for in range(40): el random choice(elements) 20.add(el) ql.add(el) for i in range(n): assert O[i] qi[i] ___iter [16] def counting_queue_iter (self): ### YOUR CODE HERE CountingQueue. _iter_ counting_queue_iter [17] # 5 points. Simple tests. q = CountingQueue () q. add("cat", count=2) q. add("dog", count=3) [x for x in q] assert == ["cat"] * 2 + ["dog"] * 3 > # 5 points. Works the same as queue. for = k in range (100): q0 Queue () q1 CountingQueue () for in range(100): el random choice(["a", "b", q0. add(el) ql.add(el) assert [x for in qo] = "C']) [x for in qi] getitem [] def counting_queue_getitem(self, n): ### YOUR CODE HERE CountingQueue. _getitem_ counting_queue_getitem # 5 points: simple tests. = q CountingQueue () q. add("cat", count=2) q.add("dog", count=3) q.add("bird", count=4) els [q[i] for i in range (9)] assert els ['cat'] * 2 + ['dog'] * 3 # Let's do it again. [q[i] for i in range (9)] assert els ['cat'] * 2 + ['dog'] * 3 = + ['bird'] * 4 els == + ['bird'] BK 4 [ ] # 5 points: you raise IndexError when accessing elements out of bounds. a = CountingQueue () q.add("cat", count=2) q.add("dog", count=3) too high... to raise IndexError" # Raise IndexError when it's try: q[5] assert False, "Failed except IndexError: pass assert q[4] "dog" try: q[5] class Stack(object): def _init__(self): self. stack [] def a us to print the repr__(self): "Defining _repr__ function will enable stack contents, and facilitate debugging.' return repr(self. stack) # Good enough. def push(self, **"The "top" of the self. stack. append(x) stack is the end of the list. def pop (self): return self. stack.pop() if len(self. stack) > 0 else None def isempty(self): return len(self. stack) == 0 def _len_(self): return len(self. stack) def Liter_(self): for el in self. stack: yield el def _getitem_(self, i): return self. stack[i] def-contains_(self, x): X in self. stack return Let's see how this works. S = Stack() print (s.pop() s. push('a') S. push('b') print(s.pop()) print (s.pop() print(s.pop()) None b a None Ok! The definition of a queue is similar. [46] class Queue (object): def __init__(self): self. queue [] def _(self): a us to print the repr "Defining _repr__ function will enable queue contents, and facilitate debugging. return repr (self. queue) # Good enough. def x): add(self, self. queue. append(x) def get (self): def __init__(self): = self. queue [] def us to print the repr_(self): ***"Defining a _repr_ function will enable queue contents, and facilitate debugging. return repr(self. queue) # Good enough. def add(self, x): self. queue. append(x) def get (self): # This is the only difference compared to the stack above. return self. queue.pop(0) if len(self. queue) > 0 else None def isempty(self): return len(self. queue) == 0 def _len_(self): len(self. queue) return def Liter__(self): for el in self. queue: yield el def _getitem__(self, i): return self. queue[i] def _contains__(self, x): return x in self. queue Let's see how it works. 47 = Queue () Let's see how it works. S Queue 0 print (s.get) S.add('a') S.add('b') print (s.get) print(s.get()) print (s.get) None a b None As you see, in a queue, the elements are retrieved in the same order in which they were added. Python experts might note that, for a queue, we would do better by using the collections, deque class, rather than the list class, to make the pop (0) operation more efficient; in lists, it takes time proportional to the length of the list; in deques, it takes constant time. For small lists, however, the difference is negligible. We now consider a use case in which we may need to put in the queue or stack many repeated copies of the same object. For instance, assume that the queue is used to store events, and assume that some event may end up being repeated many times in a row. As an example, the events can be "s", for the tick of a second, "m", when the minute advances, and "h", when the hour advances. There will be 60 consecutive "s" events between any two "m" events, and it seems a waste to store so many consecutive identical events. Storing many identical things in a row is akin to counting in unary notation, after all. We would be better off storing the repeated elements only once, along with a count of the number of times they occur let's develona queue using this ideal stack can be done similarly class CountingQueue (object): def __init__(self): self. queue = [] def _repr_(self): return repr(self. queue) same def add(self, count=1): # If the element is the as the last element, we simply # increment the count. This assumes we can test equality of # elements. if len(self. queue) > 0: CC self. queue [-1] if self. queue [-1] (xx, + count) else: self. queue. append((x, count)) else: self. queue [(x, count)] XX = CC == C = C def get (self): if len(self. queue) 0: return None self. queue [0] if 1: self. queue. pop (0) return else: self. queue [0] (x, C - 1) return def isempty(self): [] q CountingQueue () q. add("cat", count=2) q. add("dog" count=3) # Raise IndexError when it's too high... try: q[5] assert False, "Failed to raise IndexError" except IndexError: pass assert q[4] 'dog try: q[5] assert False, "Failed to raise IndexError" except IndexError: pass == # And also when it's too low. try: q[-1] assert False, "Failed to raise IndexError" except IndexError: pass a non-integer. # And raise TypeError if you try to index with try: q["hello"] assert False, "Failed to raise TypeError" except TypeError: pass [] # 5 points. Behaves the same as Queue. elements range (3) print(a) [('a', 1)] [('a', 1), ('b', 5)] [('a', 1), ('b', 5), ('0', 2)] a [('b', 5), ('c', 2)] b [('b', 4), ('0', 2)] b [('b', 3), ('0', 2)] b [('b', 2), ('c', 2)] b [('b', 1), ('0', 2)] b [('c', 2)] C ico , 1 [('c', 1)] [] It works! And notice that it works even if we add elements one by one. q = CountingQueue () for i in range(10): q. add('a') q. add('b') for i in range (3): q. add('c', count=2) print(a) - [('a', 10), ('b', 1), ('d', 6)] _len_ [12] def counting_queue_len(self): ### YOUR CODE HERE length 0 for X,C in self. queue: length+=0 return length def next (self): res= self. queue [self.n] self.n= self.n+1 return res CountingQueue. _len_ counting_queue_len # 5 points. Simple tests q CountingQueue () assert len(q) 0 q. add("cat") q. add("dog") assert len() 2 == [14] # 5 points. More complicated tests. == q CountingQueue) assert len() 0 q. add("cat") q. add("cat") assert len(q. queue) == 1 # 5 points. [14] More complicated tests. = == q CountingQueue () assert len(a) 0 q. add("cat") q. add("cat") assert len(q. queue) 1 assert len(a) 2 q. add("dog") assert len(a) 3 assert len(q. queue) 2 q. add("dog') assert len(a) 4 assert len(a) 4 # Hey, just in assert len(a) 4 assert len(q. queue) 2 == == == case you went for the quantum-mechanical solution ;-) == [15] # 5 points. Works same as Queue. import random for k in range(100): q0 Queue q1 CountingQueue () for in range(100): el random choice (["a", "b", "O"]) qo.add(el) ql.add(el) assert len(0) len(1) assert len(q0. queue) >= len(q1. queue) iter The Homework Assignment For this homework, you must implement the following methods for CountingQueue : _len__ Liter _in_ _getitem_ Your goal is to have CountingQueue behave exactly like Queue to an outside user: the objects have to be different only due to their internal implementation. So for instance, _len_ must return the number of elements, including repetitions; not the number of (element, count) pairs in self. queue. Note that we are adding methods to a class that has already been defined, so our definition have the following somewhat unusual form: == 0: def counting_queue_peek (self): if len(self. queue) return None el, self. queue [0] return el CountingQueue. peek counting_queue_peek In other words, we first create a function (in this case counting_queue_peek ) and then we assign it to the method peek of CountingQueue . It's a bit unusual, but it works, and it relieves us from the task of redefining the class each time we need a new method. [] g = CountingQueue () q. add("cat") q. add("dog") q. peek) [] q CountingQueue () q. add("cat", count=2) q. add("dog" count=3) # Raise IndexError when it's too high... try: q[5] assert False, "Failed to raise IndexError" except IndexError: pass assert q[4] 'dog try: q[5] assert False, "Failed to raise IndexError" except IndexError: pass == # And also when it's too low. try: q[-1] assert False, "Failed to raise IndexError" except IndexError: pass a non-integer. # And raise TypeError if you try to index with try: q["hello"] assert False, "Failed to raise TypeError" except TypeError: pass [] # 5 points. Behaves the same as Queue. elements range (3) [ ] # 5 points. Behaves the same as Queue. range (3) = IIL elements for k in range(100): qo Queue () q1 CountingQueue () for in range(40): el random choice(elements) 20.add(el) ql.add(el) for i in range(n): assert O[i] qi[i] ___iter [16] def counting_queue_iter (self): ### YOUR CODE HERE CountingQueue. _iter_ counting_queue_iter [17] # 5 points. Simple tests. q = CountingQueue () q. add("cat", count=2) q. add("dog", count=3) [x for x in q] assert == ["cat"] * 2 + ["dog"] * 3 > # 5 points. Works the same as queue. for = k in range (100): q0 Queue () q1 CountingQueue () for in range(100): el random choice(["a", "b", q0. add(el) ql.add(el) assert [x for in qo] = "C']) [x for in qi] getitem [] def counting_queue_getitem(self, n): ### YOUR CODE HERE CountingQueue. _getitem_ counting_queue_getitem # 5 points: simple tests. = q CountingQueue () q. add("cat", count=2) q.add("dog", count=3) q.add("bird", count=4) els [q[i] for i in range (9)] assert els ['cat'] * 2 + ['dog'] * 3 # Let's do it again. [q[i] for i in range (9)] assert els ['cat'] * 2 + ['dog'] * 3 = + ['bird'] * 4 els == + ['bird'] BK 4 [ ] # 5 points: you raise IndexError when accessing elements out of bounds. a = CountingQueue () q.add("cat", count=2) q.add("dog", count=3) too high... to raise IndexError" # Raise IndexError when it's try: q[5] assert False, "Failed except IndexError: pass assert q[4] "dog" try: q[5]