Python Programming

Please add comments

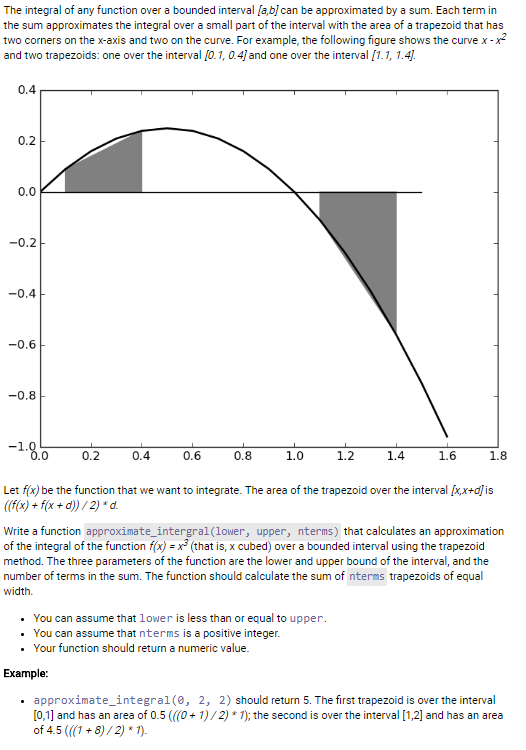
The integral of any function over a bounded interval [a,bjcan be approximated by a sum. Each term in the sum approximates the integral over a small part of the interval with the area of a trapezoid that has two corners on the x-axis and two on the curve. For example, the following figure shows the curve x-x2 and two trapezoids: one over the interval [o.1, 0.4/and one over the interval [1.1, 1.4 0.4 0.0 -0.2 -0.4 -0.6 -0.8 0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 Let f(X) be the function that we want to integrate. The area of the trapezoid over the interval p,x+d]is Write a function approximate_intergral(lower, upper, nterms) that calculates an approximation of the integral of the function f(x)x(that is, x cubed) over a bounded interval using the trapezoid method. The three parameters of the function are the lower and upper bound of the interval, and the number of terms in the sum. The function should calculate the sum of nterms trapezoids of equal width. . You can assume that lower is less than or equal to upper . You can assume that nterms is a positive integer . Your function should return a numeric value Example: . approximate_integral(0, 2, 2) should return 5. The first trapezoid is over the interval [0,1] and has an area of 0.5 (01)/2) *7); the second is over the interval [1,2] and has an area of 4.5 (1+8)/2) 1)