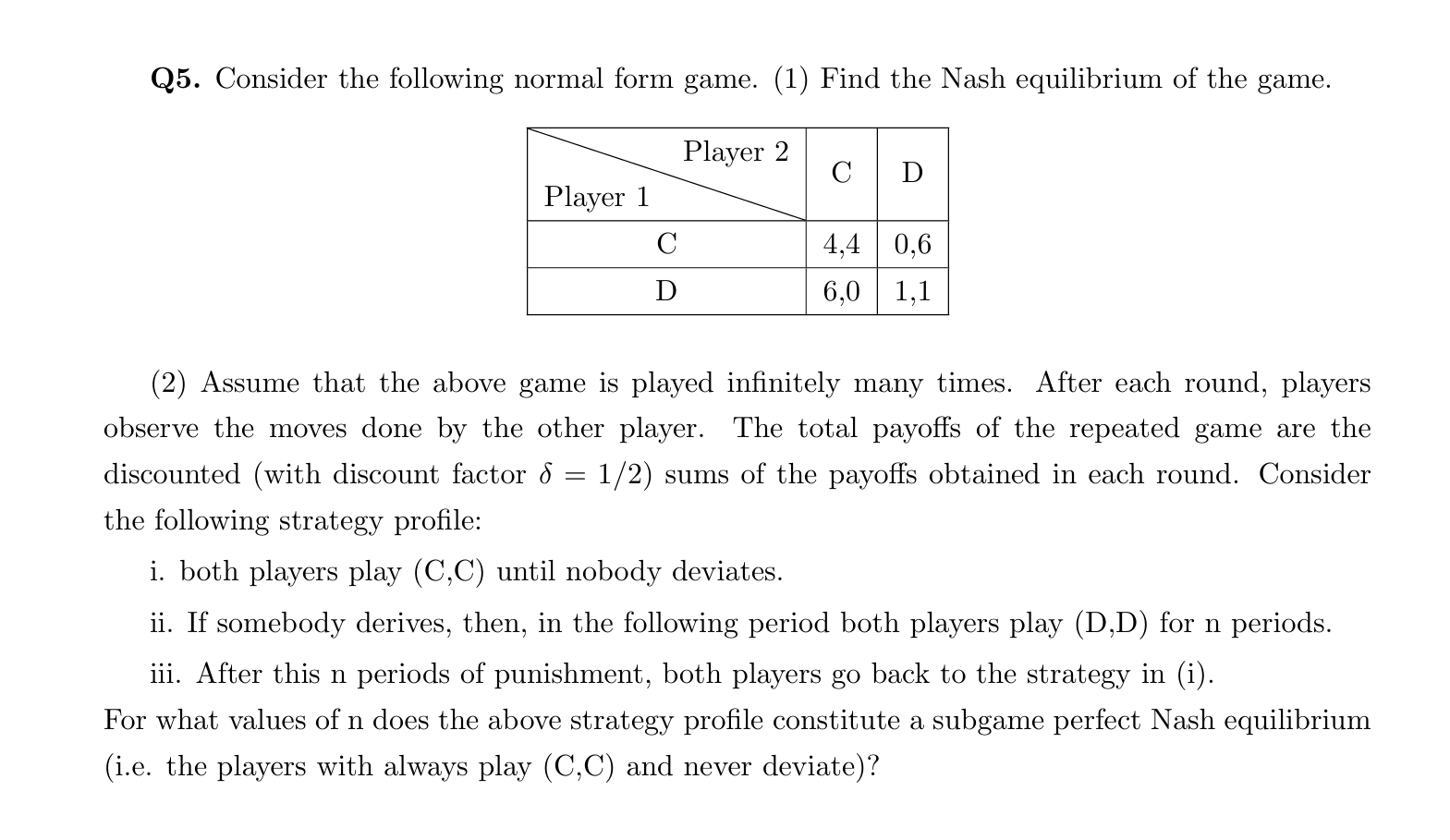
Q$5.$ Consider the following normal form game. $(1)$ Find the Nash equilibrium of the game.

$(2)$ Assume that the above game is played infinitely many times. After each round, players observe the moves done by the other player. The total payoffs of the repeated game are the discounted $($with discount factor $\backslash (\backslash$delta$=1/2\backslash ))$ sums of the payoffs obtained in each round. Consider the following strategy profile:

i$.$ both players play $($C$,$C$)$ until nobody deviates.

ii$.$ If somebody derives, then, in the following period both players play $($D$,$D$)$ for n periods.

iii. After this n periods of punishment, both players go back to the strategy in $($i$).$

For what values of n does the above strategy profile constitute a subgame perfect Nash equilibrium $($i$.$e$.$ the players with always play $($C$,$C$)$ and never deviate$)?$