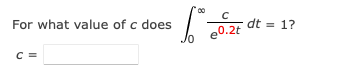
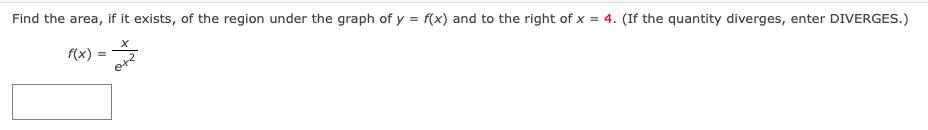
Q1Q3

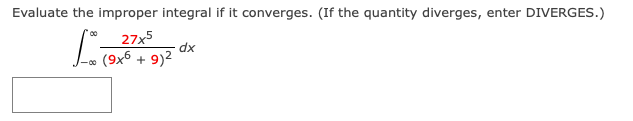
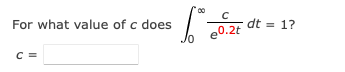
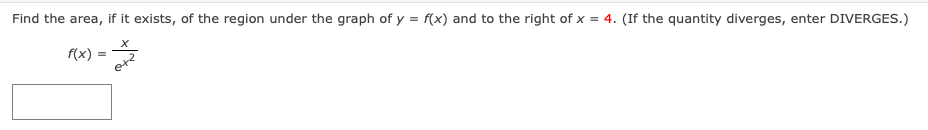
Evaluate the improper integral if it converges. (If the quantity diverges, enter DIVERGES.) 27x5 (9x6 + 9)2 dxEvaluate the improper integral if it converges. (If the quantity diverges, enter DIVERGES.) 4e-* dx 5Evaluate the improper integral if it converges. (If the quantity diverges, enter DIVERGES.) ca 1 dx XEvaluate the improper integral if it converges. (If the quantity diverges, enter DIVERGES.) 1 5 dx XEvaluate the improper integral if it converges. (If the quantity diverges, enter DIVERGES.) 8x ( x 2 + 1 ) 2 dx\fFind the area, if it exists, of the region under the graph of y = f(x) and to the right of x = 4. (If the quantity diverges, enter DIVERGES.) f(x ) = X 2Find the area, if it exists, of the region under the graph of y = f(x) and to the right of x = 1. (If the quantity diverges, enter DIVERGES.) 4 f ( x ) = xx