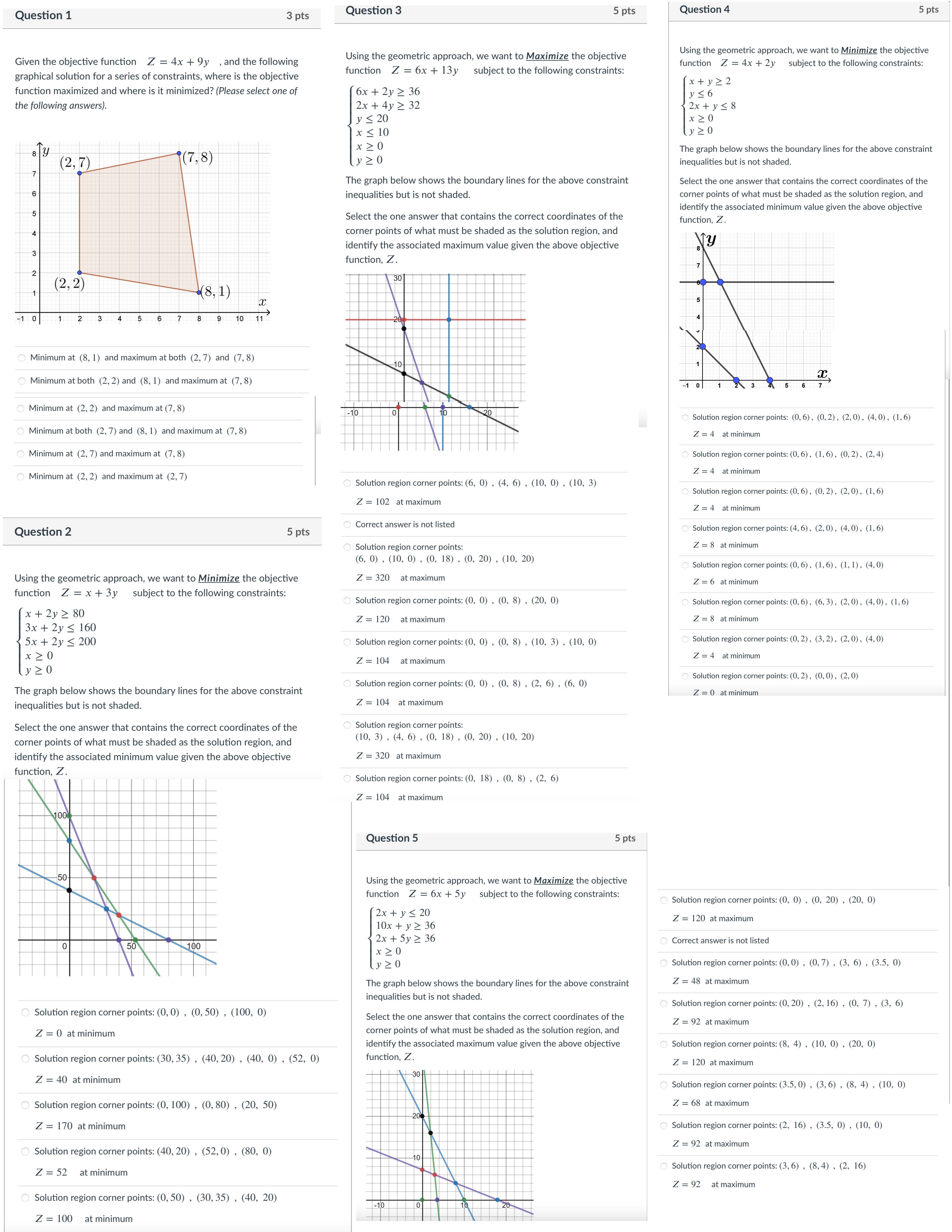
Question 1 3 pts Question 3 5 pts Question 4 5 pts Using the geometric approach, we want to Maximize the objective Using the geometric approach, we want to Minimize the objective Given the objective function Z = 4x + 9y , and the following function Z = 4x + 2y subject to the following constraints: graphical solution for a series of constraints, where is the objective function Z = 6x + 13y subject to the following constraints: [x + y 2 2 function maximized and where is it minimized? (Please select one of 6x + 2y 2 36 yS6 the following answers). 2x + 4y 2 32 2x+ys8 y S 20 x 20 x 5 10 y 20 The graph below shows the boundary lines for the above constraint ( 2 , 7 ) i (7 , 8 ) inequalities but is not shaded. The graph below shows the boundary lines for the above constraint Select the one answer that contains the correct coordinates of the inequalities but is not shaded. corner points of what must be shaded as the solution region, and identify the associated minimum value given the above objective Select the one answer that contains the correct coordinates of the function, Z. corner points of what must be shaded as the solution region, and identify the associated maximum value given the above objective Ny function, Z. (2, 2) (8, 1) 1 0 Minimum at (8, 1) and maximum at both (2, 7) and (7, 8) Minimum at both (2, 2) and (8, 1) and maximum at (7, 8) Minimum at (2, 2) and maximum at (7, 8) Solution region corner points: (0, 6), (0, 2), (2, 0), (4, 0) , (1, 6) Minimum at both (2, 7) and (8, 1) and maximum at (7, 8) Z = 4 at minimum Minimum at (2, 7) and maximum at (7, 8) Solution region corner points: (0, 6), (1, 6), (0, 2), (2, 4) Minimum at (2, 2) and maximum at (2, 7) Z = 4 at minimum Solution region corner points: (6, 0) , (4, 6) , (10, 0) , (10, 3) Solution region corner points: (0, 6) , (0, 2), (2, 0), (1, 6) Z = 102 at maximum Z = 4 at minimum Question 2 Correct answer is not listed 5 pts Solution region corner points: (4, 6) , (2, 0), (4, 0), (1, 6) Solution region corner points: Z = 8 at minimum (6, 0) , (10, 0) , (0, 18) , (0, 20) , (10, 20) Solution region corner points: (0, 6), (1, 6), (1, 1), (4, 0) Using the geometric approach, we want to Minimize the objective Z = 320 at maximum Z = 6 at minimum function Z = x+ 3y subject to the following constraints: Solution region corner points: (0, 0) , (0, 8) , (20, 0) Solution region corner points: (0, 6), (6, 3), (2, 0), (4,0), (1, 6) x + 2y 2 80 Z = 120 at maximum Z = 8 at minimum 3x + 2y = 160 5x + 2y S 200 Solution region corner points: (0, 0) , (0, 8) , (10, 3) , (10, 0) Solution region corner points: (0, 2) , (3, 2), (2, 0), (4, 0) x 20 = 104 at maximum Z = 4 at minimum 20 Solution region corner points: (0, 0) , (0, 8) , (2, 6) , (6, 0) Solution region corner points: (0, 2) , (0, 0), (2, 0) The graph below shows the boundary lines for the above constraint Z = 0 at minimum inequalities but is not shaded. Z = 104 at maximum Select the one answer that contains the correct coordinates of the Solution region corner points: corner points of what must be shaded as the solution region, and (10, 3) , (4, 6) , (0, 18) , (0, 20) , (10, 20) identify the associated minimum value given the above objective Z = 320 at maximum function, Z. Solution region corner points: (0, 18) , (0, 8) , (2, 6) Z = 104 at maximum Question 5 5 pts 50 Using the geometric approach, we want to Maximize the objective function Z = 6x + 5y subject to the following constraints: Solution region corner points: (0, 0) , (0, 20) , (20, 0) 2x+ y 36 Correct answer is not listed x 20 y 20 Solution region corner points: (0, 0) , (0, 7) , (3, 6) , (3.5, 0) The graph below shows the boundary lines for the above constraint Z = 48 at maximum inequalities but is not shaded. Solution region corner points: (0, 20) , (2, 16) , (0, 7) , (3, 6) Solution region corner points: (0, 0) , (0, 50) , (100, 0) Select the one answer that contains the correct coordinates of the Z = 92 at maximum Z = 0 at minimum corner points of what must be shaded as the solution region, and identify the associated maximum value given the above objective Solution region corner points: (8, 4) , (10, 0) , (20, 0) Solution region corner points: (30, 35) , (40, 20) , (40, 0) , (52, 0) function, Z. Z = 120 at maximum Z = 40 at minimum Solution region corner points: (3.5, 0) , (3, 6) , (8, 4) , (10, 0) Solution region corner points: (0, 100) , (0, 80) , (20, 50) Z = 68 at maximum Z = 170 at minimum Solution region corner points: (2, 16) , (3.5, 0) , (10, 0) Solution region corner points: (40, 20) , (52, 0) , (80, 0) Z = 92 at maximum Z = 52 at minimum Solution region corner points: (3, 6) , (8,4) , (2, 16) Z = 92 at maximum Solution region corner points: (0, 50) , (30, 35) , (40, 20) Z = 100 at minimum