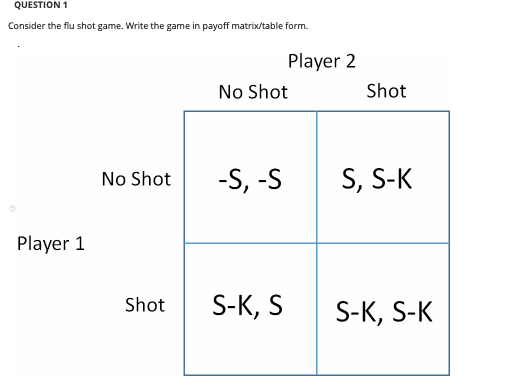
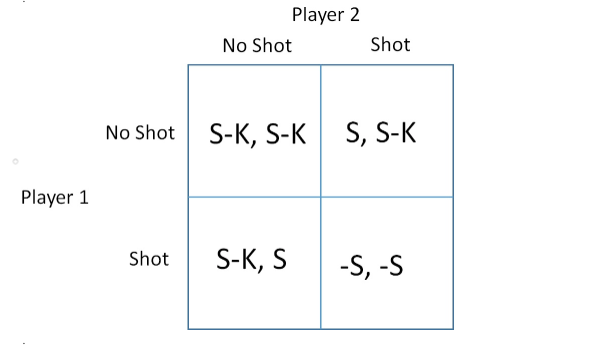
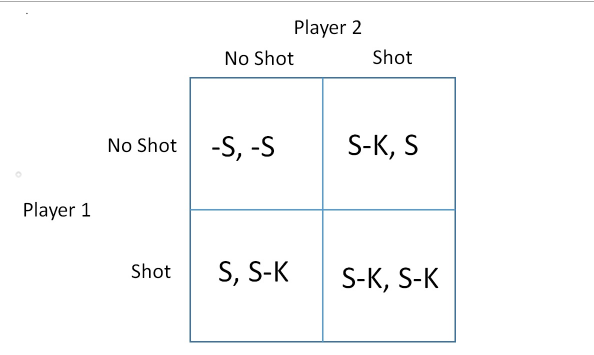
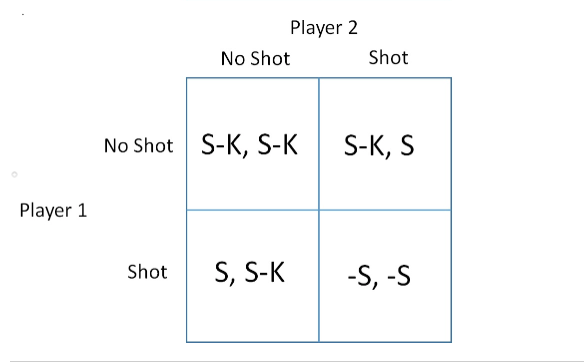
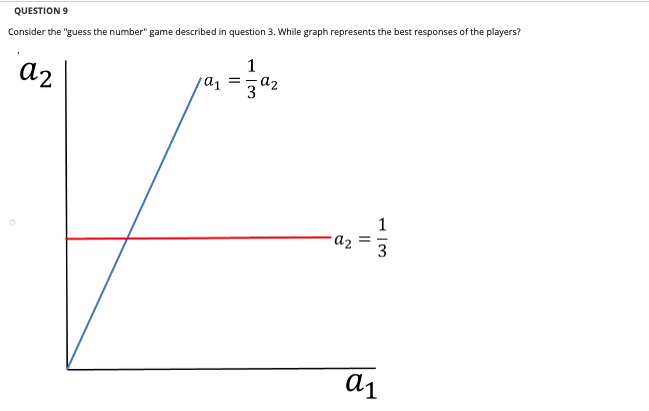
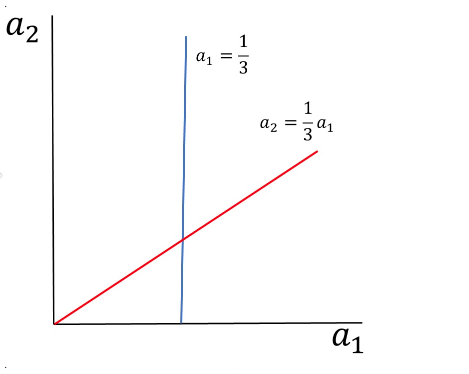
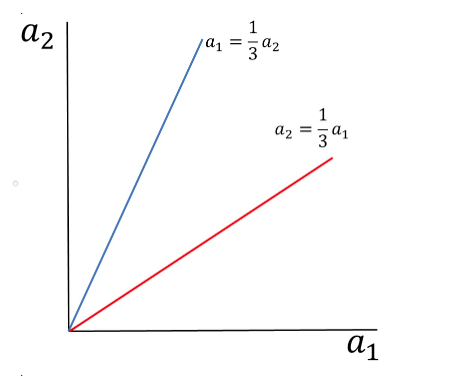
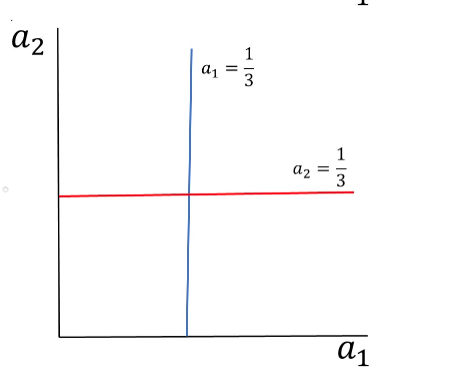
QUESTION 1 Consider the flu shot game. Write the game in payoff matrix/table form. Player 2 No Shot Shot No Shot -S, -S S, S-K Player 1 Shot S-K, S S-K, S-K Player 2 No Shot Shot No Shot S-K, S-K S-K, S-K S, S-K Player 1 Shot S-K, S -S, -S Player 2 No Shot Shot No Shot -S, -S S-K, S Player 1 Shot S, S-K S-K, S-K Player 2 No Shot Shot No Shot S-K, S-K S-K, S Player 1 Shot S, S-K -S, -S QUESTION 2 Consider each player's best response function. What is Player 1's best response when Player 2 chooses to get the shot? Get the shot. Not get the shot. Both get the shot and not get the shot. Neither get the shot or get the shot. QUESTION 3 Consider each player's best response function. What is Player 1's best response when Player 2 chooses to not get the shot? Get the shot. Not get the shot. Both get the shot and not get the shot. Neither get the shot or get the shot. QUESTION 4 What are the Nash equilibria in this game? Both (P1=Shot, P2=Shot) and (P1=No shot, P2=No shot) Only (P1=Shot, P2-No shot) Both (P1=Shot, P2=No shot) and (P1=No shot, P2=shot) Only (P1=No shot, P2-shot) QUESTIONS Which statement best describes the implications of the Nash equilibria in this game? Nobody will get shots, and society will be better off. Everybody will get shots, and society will be better off. Everybody will get shots, and society will be worse off. . Some people will get shots, while others don't, because of a "free rider effect". QUESTION 6 Consider the game in Question 2. For which values of e is the strategy profile (Player 1=B, Player 2=B) the only Nash equilibrium? Alle less than 4. All e greater than 4 No solution exists. All possible values of e. QUESTION 7 Consider the game in Question 2. For which values of e are the strategy profiles (Player 1=A, Player 2=B) and (Player 1=B, Player 2=A) the only Nash equilibria? All possible values of e. No solution exists. All e greater than 4 Alle less than 4 QUESTIONS Consider the game in Question 2. For which values of e are the strategy profiles (Player 1=A, Player 2=B). (Player 1=B, Player 2=A), and (Player 1=B, Player 2=B) all Nash equilibria? All possible values of e. No solution exists. e equal to 2 e equal to 4 QUESTION 9 Consider the "guess the number" game described in question 3. While graph represents the best responses of the players? A2 1 a2 a1 a2 II A1 a2 au 1 3 1 az = 301 di 1 a2 101 = 1 02 -304 a1 02 1 41 || 3 || 42 41 QUESTION 10 Consider the guess the number game described in question 3. What is the Nash equilibrium in this game? (P1=0, P2=0) (P1-1/3, P2=0) (P1=0, P2=1/3) (P1-1/3, P2=1/3) QUESTION 11 Consider the 3 player game considered in question 4. What is Player 1's best response when Player 2 chooses right, and Player 3 chooses right? Left Right Up Down QUESTION 12 Consider the 3 player game considered in question 4. What is Player 2's best response when Player 1 chooses up, and Player 3 chooses right? Left Right Up Down QUESTION 13 Consider the 3 player game considered in question 4. What is Player 3's best response when Player 1 chooses up, and Player 2 chooses left? Left Right Up Down QUESTION 14 Consider the 3 player game considered in question 4. What is Player 2's best response when Player 1 chooses down, and Player 3 chooses right? Up Down Left Right QUESTION 15 Consider the 3 player game considered in question 4. Is the following a Nash equilibrium? (Player 1=Down, Player 2=Right, Player 3-Left)? Yes. No. QUESTION 16 Consider the 3 player game considered in question 4. Is the following a Nash equilibrium? (Player 1=Up, Player 2=Right, Player 3=Left)? Yes. No. QUESTION 17 Consider the 3 player game considered in question 4. Is the following a Nash equilibrium? (Player 1=Down, Player 2=Right, Player 3=Right)? Yes. No. QUESTION 1 Consider the flu shot game. Write the game in payoff matrix/table form. Player 2 No Shot Shot No Shot -S, -S S, S-K Player 1 Shot S-K, S S-K, S-K Player 2 No Shot Shot No Shot S-K, S-K S-K, S-K S, S-K Player 1 Shot S-K, S -S, -S Player 2 No Shot Shot No Shot -S, -S S-K, S Player 1 Shot S, S-K S-K, S-K Player 2 No Shot Shot No Shot S-K, S-K S-K, S Player 1 Shot S, S-K -S, -S QUESTION 2 Consider each player's best response function. What is Player 1's best response when Player 2 chooses to get the shot? Get the shot. Not get the shot. Both get the shot and not get the shot. Neither get the shot or get the shot. QUESTION 3 Consider each player's best response function. What is Player 1's best response when Player 2 chooses to not get the shot? Get the shot. Not get the shot. Both get the shot and not get the shot. Neither get the shot or get the shot. QUESTION 4 What are the Nash equilibria in this game? Both (P1=Shot, P2=Shot) and (P1=No shot, P2=No shot) Only (P1=Shot, P2-No shot) Both (P1=Shot, P2=No shot) and (P1=No shot, P2=shot) Only (P1=No shot, P2-shot) QUESTIONS Which statement best describes the implications of the Nash equilibria in this game? Nobody will get shots, and society will be better off. Everybody will get shots, and society will be better off. Everybody will get shots, and society will be worse off. . Some people will get shots, while others don't, because of a "free rider effect". QUESTION 6 Consider the game in Question 2. For which values of e is the strategy profile (Player 1=B, Player 2=B) the only Nash equilibrium? Alle less than 4. All e greater than 4 No solution exists. All possible values of e. QUESTION 7 Consider the game in Question 2. For which values of e are the strategy profiles (Player 1=A, Player 2=B) and (Player 1=B, Player 2=A) the only Nash equilibria? All possible values of e. No solution exists. All e greater than 4 Alle less than 4 QUESTIONS Consider the game in Question 2. For which values of e are the strategy profiles (Player 1=A, Player 2=B). (Player 1=B, Player 2=A), and (Player 1=B, Player 2=B) all Nash equilibria? All possible values of e. No solution exists. e equal to 2 e equal to 4 QUESTION 9 Consider the "guess the number" game described in question 3. While graph represents the best responses of the players? A2 1 a2 a1 a2 II A1 a2 au 1 3 1 az = 301 di 1 a2 101 = 1 02 -304 a1 02 1 41 || 3 || 42 41 QUESTION 10 Consider the guess the number game described in question 3. What is the Nash equilibrium in this game? (P1=0, P2=0) (P1-1/3, P2=0) (P1=0, P2=1/3) (P1-1/3, P2=1/3) QUESTION 11 Consider the 3 player game considered in question 4. What is Player 1's best response when Player 2 chooses right, and Player 3 chooses right? Left Right Up Down QUESTION 12 Consider the 3 player game considered in question 4. What is Player 2's best response when Player 1 chooses up, and Player 3 chooses right? Left Right Up Down QUESTION 13 Consider the 3 player game considered in question 4. What is Player 3's best response when Player 1 chooses up, and Player 2 chooses left? Left Right Up Down QUESTION 14 Consider the 3 player game considered in question 4. What is Player 2's best response when Player 1 chooses down, and Player 3 chooses right? Up Down Left Right QUESTION 15 Consider the 3 player game considered in question 4. Is the following a Nash equilibrium? (Player 1=Down, Player 2=Right, Player 3-Left)? Yes. No. QUESTION 16 Consider the 3 player game considered in question 4. Is the following a Nash equilibrium? (Player 1=Up, Player 2=Right, Player 3=Left)? Yes. No. QUESTION 17 Consider the 3 player game considered in question 4. Is the following a Nash equilibrium? (Player 1=Down, Player 2=Right, Player 3=Right)? Yes. No