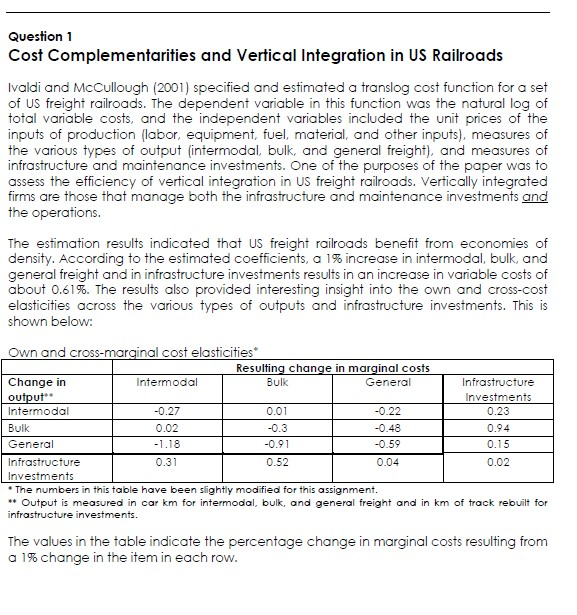
Question 1 Cost Complementarities and Vertical Integration in US Railroads Ivaldi and McCullough (2001) specified and estimated a translog cost function for a set of US freight railroads. The dependent variable in this function was the natural log of total variable costs, and the independent variables included the unit prices of the inputs of production (labor, equipment, fuel, material, and other inputs), measures of the various types of output (intermodal, bulk, and general freight), and measures of infrastructure and maintenance investments. One of the purposes of the paper was to assess the efficiency of vertical integration in US freight railroads. Vertically integrated firms are those that manage both the infrastructure and maintenance investments and the operations. The estimation results indicated that US freight railroads benefit from economies of density. According to the estimated coefficients, a 1% increase in intermodal, bulk, and general freight and in infrastructure investments results in an increase in variable costs of about 0.61%. The results also provided interesting insight into the own and cross-cost elasticities across the various types of outputs and infrastructure investments. This is shown below: Own and cross-marginal cost elasticities Resulting change in marginal costs Change in Intermodal Bulk General Infrastructure output Investments Intermodal -0.27 0.01 -0.22 0.23 Bulk 0.02 -0.3 -0.48 0.94 General -1.18 -0.91 -0.59 0.15 Infrastructure 0.31 0.52 0.04 0.02 Investments * The numbers in this table have been slightly modified for this assignment. * Output is measured in car km for intermodal, bulk, and general freight and in km of track rebuilt for infrastructure investments. The values in the table indicate the percentage change in marginal costs resulting from a 1% change in the item in each row. Answer the following questions: [Keep in mind that the values in the table represent elasticities with respect to marginal (not total) costs with respect to changes in output.) As mentioned above, there are economies of density when we consider a proportional increase in all outputs, as well as infrastructure investments. Do economies of density also exist for individual types of outputs (i.e. intermodal, bulk, and general freight separately)? Support your answer with estimates from the table. b. Describe any cost complementarities or anti-complementarities that you see across the various output types and infrastructure investments in the table. Briefly discuss why you think such relationships exist? Minimizing costs requires prioritizing business decisions related to infrastructure and maintenance investments and operations. This, in turn, requires coordination among various entities. Based on your answer in (b), do you think vertical integration would be efficient in US freight railroads? In other words, would total costs be minimized if infrastructure and maintenance investment decisions were made within the same company that operates the railroad, or would it be better to have two separate entities, one for operations and the other for infrastructure and maintenance investments? C. Question 1 Cost Complementarities and Vertical Integration in US Railroads Ivaldi and McCullough (2001) specified and estimated a translog cost function for a set of US freight railroads. The dependent variable in this function was the natural log of total variable costs, and the independent variables included the unit prices of the inputs of production (labor, equipment, fuel, material, and other inputs), measures of the various types of output (intermodal, bulk, and general freight), and measures of infrastructure and maintenance investments. One of the purposes of the paper was to assess the efficiency of vertical integration in US freight railroads. Vertically integrated firms are those that manage both the infrastructure and maintenance investments and the operations. The estimation results indicated that US freight railroads benefit from economies of density. According to the estimated coefficients, a 1% increase in intermodal, bulk, and general freight and in infrastructure investments results in an increase in variable costs of about 0.61%. The results also provided interesting insight into the own and cross-cost elasticities across the various types of outputs and infrastructure investments. This is shown below: Own and cross-marginal cost elasticities Resulting change in marginal costs Change in Intermodal Bulk General Infrastructure output Investments Intermodal -0.27 0.01 -0.22 0.23 Bulk 0.02 -0.3 -0.48 0.94 General -1.18 -0.91 -0.59 0.15 Infrastructure 0.31 0.52 0.04 0.02 Investments * The numbers in this table have been slightly modified for this assignment. * Output is measured in car km for intermodal, bulk, and general freight and in km of track rebuilt for infrastructure investments. The values in the table indicate the percentage change in marginal costs resulting from a 1% change in the item in each row. Answer the following questions: [Keep in mind that the values in the table represent elasticities with respect to marginal (not total) costs with respect to changes in output.) As mentioned above, there are economies of density when we consider a proportional increase in all outputs, as well as infrastructure investments. Do economies of density also exist for individual types of outputs (i.e. intermodal, bulk, and general freight separately)? Support your answer with estimates from the table. b. Describe any cost complementarities or anti-complementarities that you see across the various output types and infrastructure investments in the table. Briefly discuss why you think such relationships exist? Minimizing costs requires prioritizing business decisions related to infrastructure and maintenance investments and operations. This, in turn, requires coordination among various entities. Based on your answer in (b), do you think vertical integration would be efficient in US freight railroads? In other words, would total costs be minimized if infrastructure and maintenance investment decisions were made within the same company that operates the railroad, or would it be better to have two separate entities, one for operations and the other for infrastructure and maintenance investments? C