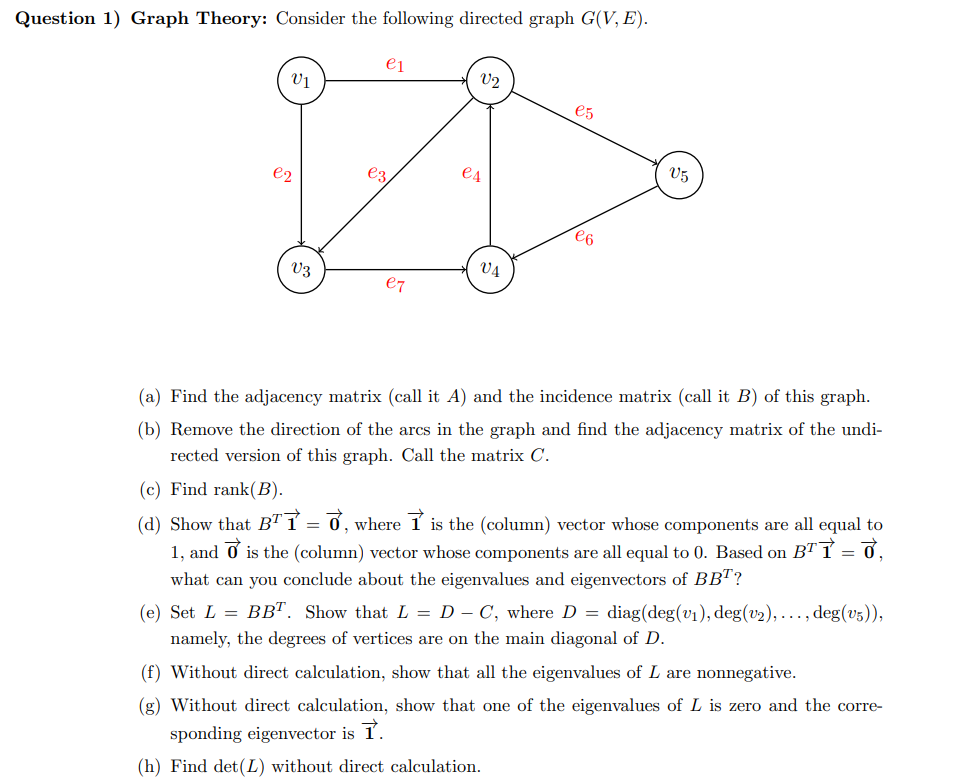
Question 1) Graph Theory: Consider the following directed graph C(V, E). (a) Find the adjacency matrix (call it A] and the incidence matrix (call it B] of this graph. (b) Remove the direction of the arcs in the graph and nd the adjacency matrix of the undi- rected version of this graph. Call the matrix C. (c) Find rank{B). (d) Show that. 3T? = 1. and W is the {column} vector whose components are all equal to D. Based on BTT = T3). > } I] . where 1 is the (column) vector whose components are all equal to what can you conclude about the eigenvalues and eigenvectors of BET? (e) Set L : BBT. Show that. L = D C. where D : diag(deg(c1],deg(cg}....,deg{1!5]). namely, the degrees of vertices are on the main diagonal of D. (f) 'Nithout direct calculation. show that all the eigenvalues of L are nonnegative. (g) W'ithout direct. calculation. show that one of the eigenvalues of L is zero and the corre- sponding eigenvector 1s 1 . (h) Find det(L) without direct. calculation