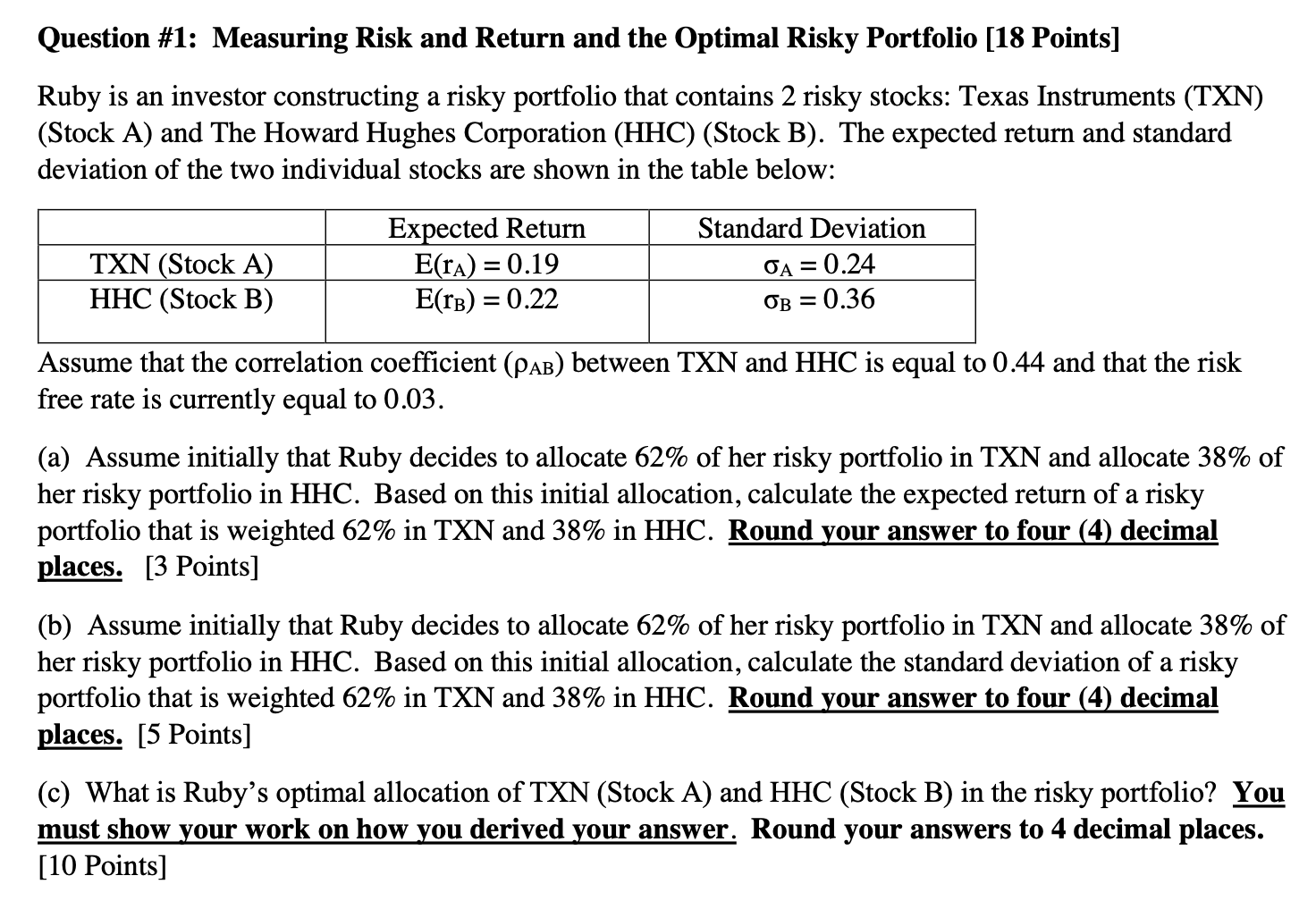
Question \\#1: Measuring Risk and Return and the Optimal Risky Portfolio [18 Points] Ruby is an investor constructing a risky portfolio that contains 2 risky stocks: Texas Instruments (TXN) (Stock A) and The Howard Hughes Corporation (HHC) (Stock B). The expected return and standard deviation of the two individual stocks are shown in the table below: Assume that the correlation coefficient \\( \\left(\ ho_{\\mathrm{AB}}\ ight) \\) between TXN and HHC is equal to 0.44 and that the risk free rate is currently equal to 0.03 . (a) Assume initially that Ruby decides to allocate \62 of her risky portfolio in TXN and allocate \38 of her risky portfolio in HHC. Based on this initial allocation, calculate the expected return of a risky portfolio that is weighted \62 in TXN and \38 in HHC. Round your answer to four (4) decimal places. [3 Points] (b) Assume initially that Ruby decides to allocate \62 of her risky portfolio in TXN and allocate \38 of her risky portfolio in HHC. Based on this initial allocation, calculate the standard deviation of a risky portfolio that is weighted \62 in TXN and \38 in HHC. Round your answer to four (4) decimal places. [5 Points] (c) What is Ruby's optimal allocation of TXN (Stock A) and HHC (Stock B) in the risky portfolio? You must show your work on how you derived your answer. Round your answers to 4 decimal places. [10 Points]