QUESTION $2(25$ MARKS$)$

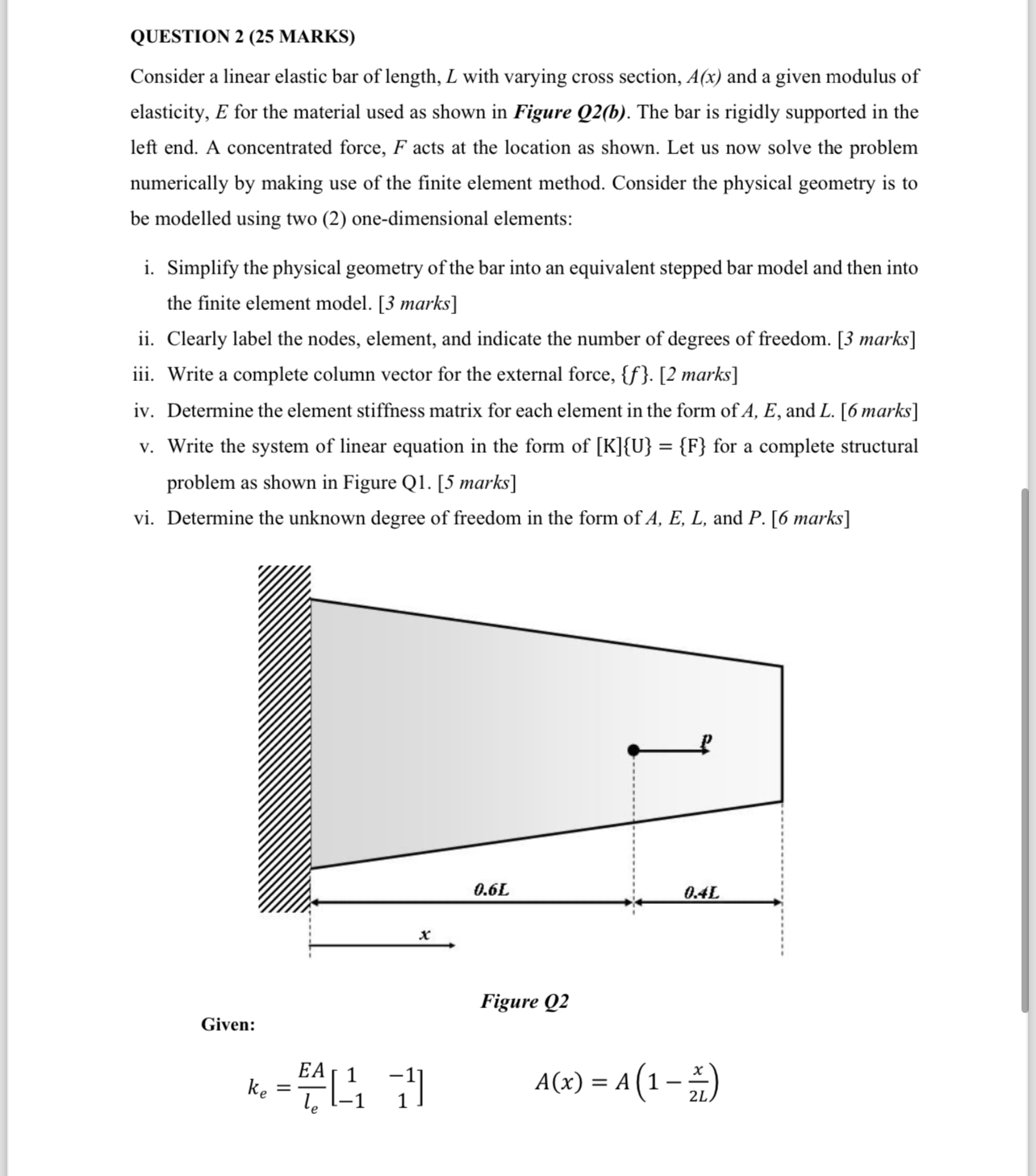
Consider a linear elastic bar of length, $L$ with varying cross section, $A(x)$ and a given modulus of elasticity, E for the material used as shown in Figure Q$2($b$).$ The bar is rigidly supported in the left end. A concentrated force, $F$ acts at the location as shown. Let us now solve the problem numerically by making use of the finite element method. Consider the physical geometry is to be modelled using two $(2)$ one$-$dimensional elements:

i$.$ Simplify the physical geometry of the bar into an equivalent stepped bar model and then into the finite element model. $[3$ marks$]$

ii$.$ Clearly label the nodes, element, and indicate the number of degrees of freedom. $[3$ marks$]$

iii. Write a complete column vector for the external force, $\{f\}.[2$ marks$]$

iv$.$ Determine the element stiffness matrix for each element in the form of $A,E,$ and $L.[6$ marks$]$

v$.$ Write the system of linear equation in the form of $[K]\{U\}=\{F\}$ for a complete structural problem as shown in Figure Q$1.[5$ marks$]$

vi$.$ Determine the unknown degree of freedom in the form of $A,E,L,$ and $P.[6$ marks$]$

Given:

$k_e=\frac{EA}{l_e}\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right],A(x)=A(1-\frac{x}{2L})$