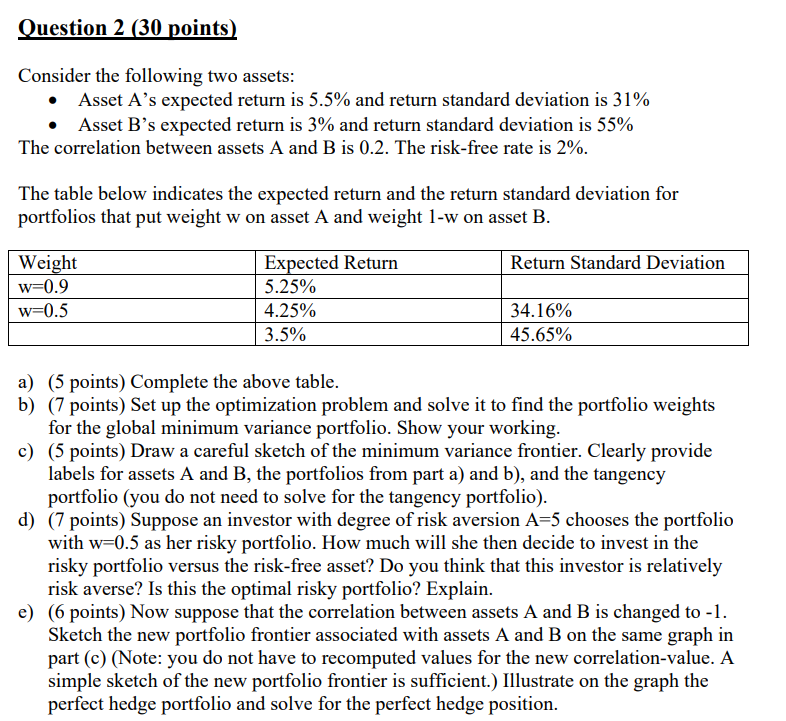
Question 2 ( 30 points) Consider the following two assets: - Asset A's expected return is 5.5\% and return standard deviation is 31% - Asset B's expected return is 3\% and return standard deviation is 55% The correlation between assets A and B is 0.2 . The risk-free rate is 2%. The table below indicates the expected return and the return standard deviation for portfolios that put weight w on asset A and weight 1-w on asset B. a) (5 points) Complete the above table. b) (7 points) Set up the optimization problem and solve it to find the portfolio weights for the global minimum variance portfolio. Show your working. c) (5 points) Draw a careful sketch of the minimum variance frontier. Clearly provide labels for assets A and B, the portfolios from part a) and b), and the tangency portfolio (you do not need to solve for the tangency portfolio). d) (7 points) Suppose an investor with degree of risk aversion A=5 chooses the portfolio with w=0.5 as her risky portfolio. How much will she then decide to invest in the risky portfolio versus the risk-free asset? Do you think that this investor is relatively risk averse? Is this the optimal risky portfolio? Explain. e) (6 points) Now suppose that the correlation between assets A and B is changed to -1 . Sketch the new portfolio frontier associated with assets A and B on the same graph in part (c) (Note: you do not have to recomputed values for the new correlation-value. A simple sketch of the new portfolio frontier is sufficient.) Illustrate on the graph the perfect hedge portfolio and solve for the perfect hedge position