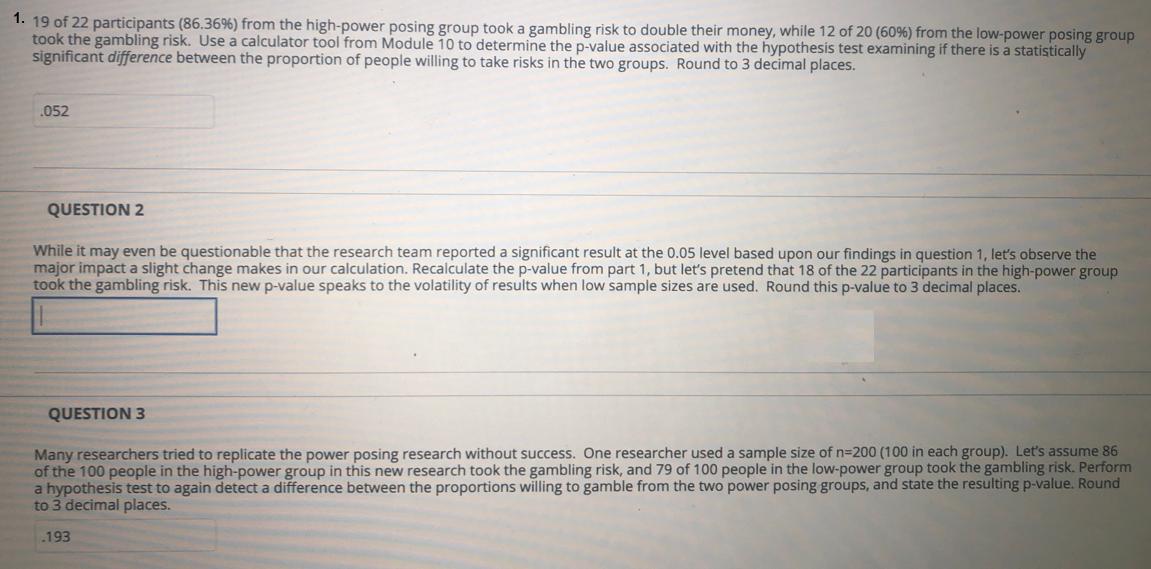
1. 19 of 22 participants (86.36%) from the high-power posing group took a gambling risk to double their money, while 12 of 20 (60%) from the low-power posing group took the gambling risk. Use a calculator tool from Module 10 to determine the p-value associated with the hypothesis test examining if there is a statistically significant difference between the proportion of people willing to take risks in the two groups. Round to 3 decimal places. .052 QUESTION 2 While it may even be questionable that the research team reported a significant result at the 0.05 level based upon our findings in question 1, let's observe the major impact a slight change makes in our calculation. Recalculate the p-value from part 1, but let's pretend that 18 of the 22 participants in the high-power group took the gambling risk. This new p-value speaks to the volatility of results when low sample sizes are used. Round this p-value to 3 decimal places. QUESTION 3 Many researchers tried to replicate the power posing research without success. One researcher used a sample size of n=200 (100 in each group). Let's assume 86 of the 100 people in the high-power group in this new research took the gambling risk, and 79 of 100 people in the low-power group took the gambling risk. Perform a hypothesis test to again detect a difference between the proportions willing to gamble from the two power posing groups, and state the resulting p-value. Round to 3 decimal places. .193