Question $3$: Fast Ancestry

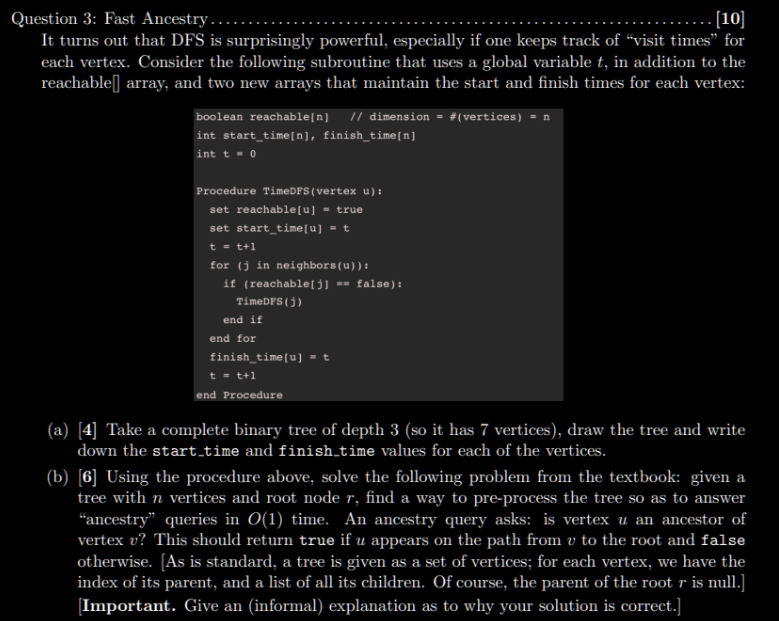
It turns out that DFS is surprisingly powerful, especially if one keeps track of "visit times" for each vertex. Consider the following subroutine that uses a global variable $\backslash ($ t $\backslash ),$ in addition to the reachable$[]$ array, and two new arrays that maintain the start and finish times for each vertex:

$```$

boolean reachable$[$n$]//$ dimension $=$ #$($vertices$)=$ n

int start$\_$time$[$n$],$ finish$\_$time$[$n$]$

int t $=0$

Procedure TimeDFS$($vertex u$)$:

set reachable$[$u$]=$ true

set start$\_$time$[$u$]=$ t

t $=$ t$+1$

for $($j in neighbors$($u$))$:

if $($reachable$[$j$]==$ false$)$:

TimeDFS$($j$)$

end if

end for

finish$\_$time$[$u$]=$ t

t $=$ t$+1$

end Procedure

$```$

$($a$)[4]$ Take a complete binary tree of depth $3($so it has $7$ vertices$),$ draw the tree and write down the start$\_$time and finish$\_$time values for each of the vertices.

$($b$)[6]$ Using the procedure above, solve the following problem from the textbook: given a tree with $\backslash ($ n $\backslash )$ vertices and root node $\backslash ($ r $\backslash ),$ find a way to pre$-$process the tree so as to answer "ancestry" queries in $\backslash ($ O$(1)\backslash )$ time. An ancestry query asks: is vertex $\backslash ($ u $\backslash )$ an ancestor of vertex $\backslash ($ v $\backslash )?$ This should return true if $\backslash ($ u $\backslash )$ appears on the path from $\backslash ($ v $\backslash )$ to the root and false otherwise. $[$As is standard, a tree is given as a set of vertices; for each vertex, we have the index of its parent, and a list of all its children. Of course, the parent of the root $\backslash ($ r $\backslash )$ is null.$][$Important$.$ Give an $($informal$)$ explanation as to why your solution is correct.$]$