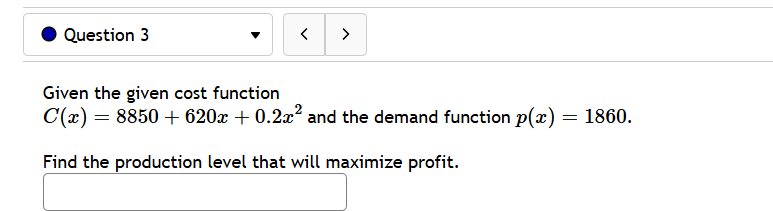
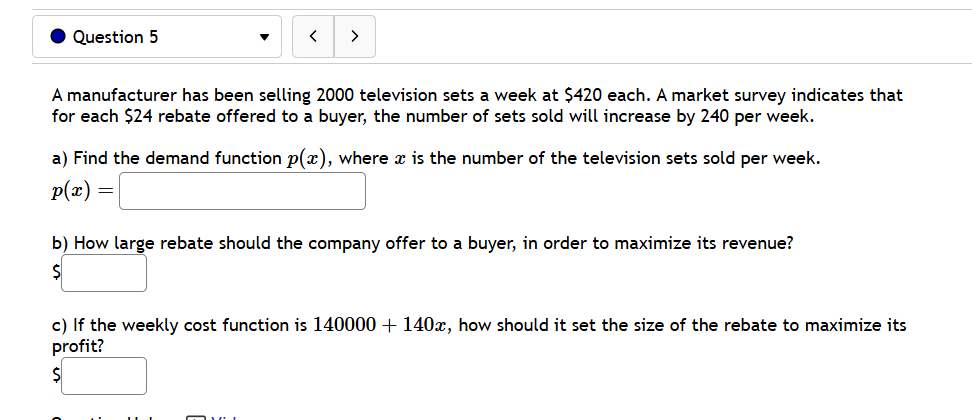
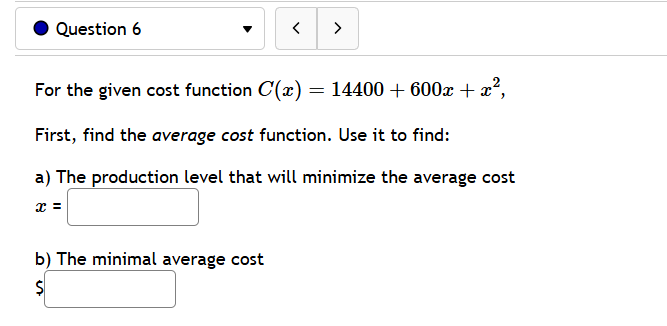
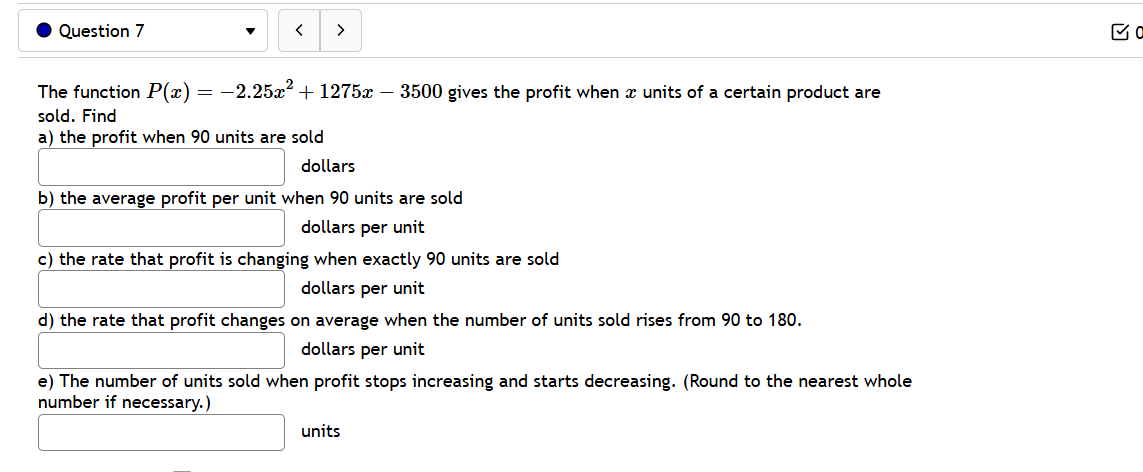
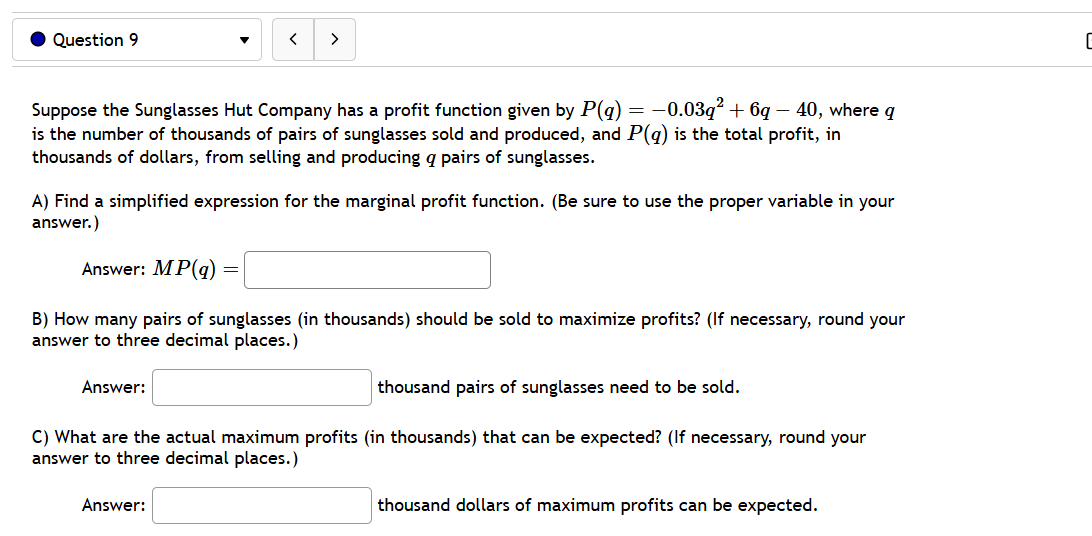
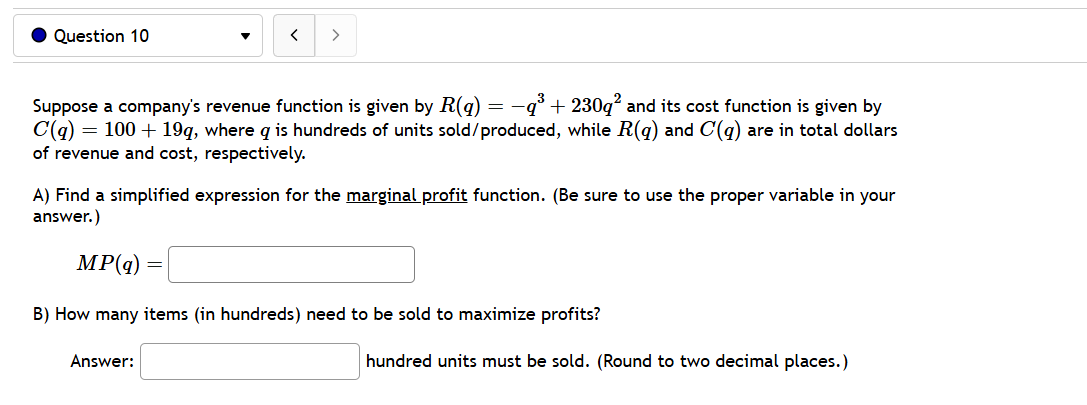
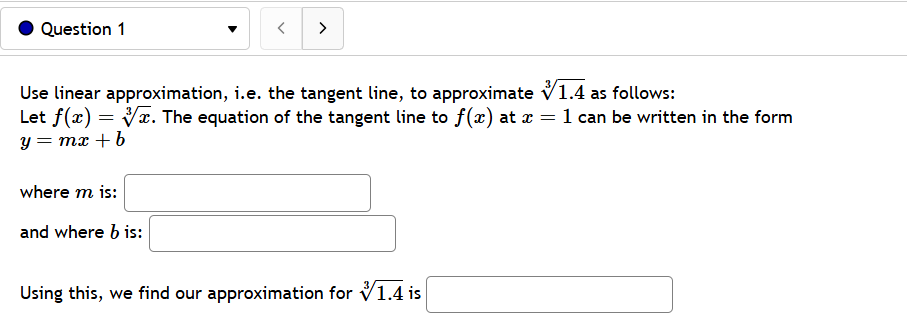
@ Question 3 v Given the given cost function C(z) = 8850 + 620z + 0.2z and the demand function p(z) = 1860. Find the production level that will maximize profit. @ Question 4 v A baseball team plays in a stadium that holds 46000 spectators. With the ticket price at $9 the average attendance has been 19000. When the price dropped to $6, the average attendance rose to 23000. Assume that attendance is linearly related to ticket price. What ticket price would maximize revenue? $ @ Question 5 v A manufacturer has been selling 2000 television sets a week at 5420 each. A market survey indicates that for each $24 rebate offered to a buyer, the number of sets sold will increase by 240 per week. a) Find the demand function p(z), where x is the number of the television sets sold per week. p(z) =| | b) How large rebate should the company offer to a buyer, in order to maximize its revenue? | c) If the weekly cost function is 140000 4 140z, how should it set the size of the rebate to maximize its profit? | - A [ e @ Question 6 v For the given cost function C(z) = 14400 + 600z + =2, First, find the average cost function. Use it to find: a) The production level that will minimize the average cost == | b) The minimal average cost | . Question 7 The function P(x) = -2.25x + 1275x - 3500 gives the profit when a units of a certain product are sold. Find a) the profit when 90 units are sold dollars b) the average profit per unit when 90 units are sold dollars per unit c) the rate that profit is changing when exactly 90 units are sold dollars per unit d) the rate that profit changes on average when the number of units sold rises from 90 to 180. dollars per unit e) The number of units sold when profit stops increasing and starts decreasing. (Round to the nearest whole number if necessary.) units@ Question 8 v Glorious Gadgets is a retailer of astronomy equipment. They purchase equipment from a supplier and then sell it to customers in their store. The function C(z) = 3z + 11250z ' + 4500 models their total inventory costs (in dollars) as a function of x the lot size for each of their orders from the supplier. The inventory costs include such things as purchasing, processing, shipping, and storing the equipment. What lot size should Glericus Gadgets order to minimize their total inventory costs? (NOTE: your answer must be the whole number that corresponds to the lowest cost.) What is their minimum total inventory cost? $ @ Question 9 v Suppose the Sunglasses Hut Company has a profit function given by P(q) = '.03(12 + 6 40, where is the number of thousands of pairs of sunglasses sold and produced, and P(q) is the total profit, in thousands of dollars, from selling and preducing g pairs of sunglasses. A) Find a simplified expression for the marginal profit function. (Be sure to use the proper variable in your answer.) Answer: M P(q) z' B) How many pairs of sunglasses (in thousands) should be sold to maximize profits? (If necessary, round your answer to three decimal places.) Answer: thousand pairs of sunglasses need to be sold. C) What are the actual maximum profits (in thousands) that can be expected? (If necessary, round your answer to three decimal places.) Answer: thousand dollars of maximum profits can be expected. @ Question 10 v Suppose a company's revenue function is given by R(g) = q3 + 2309'2 and its cost function is given by C(g) = 100 + 19g, where g is hundreds of units sold/produced, while R(g) and C(q) are in total dollars of revenue and cost, respectively. A) Find a simplified expression for the marginal profit function. (Be sure to use the proper variable in your answer.) MP(q) = B) How many items (in hundreds) need to be sold to maximize profits? Answer: hundred units must be sold. (Round to two decimal places.) @ Question 1 v Use linear approximation, i.e. the tangent line, to approximate v'1.4 as follows: Let f(a':) = /x. The equation of the tangent line to f(:.e) at x = 1 can be written in the form y=mzx+b where m is: | | and where b is: ' ' Using this, we find our approximation for V14 i5|