Question $4$

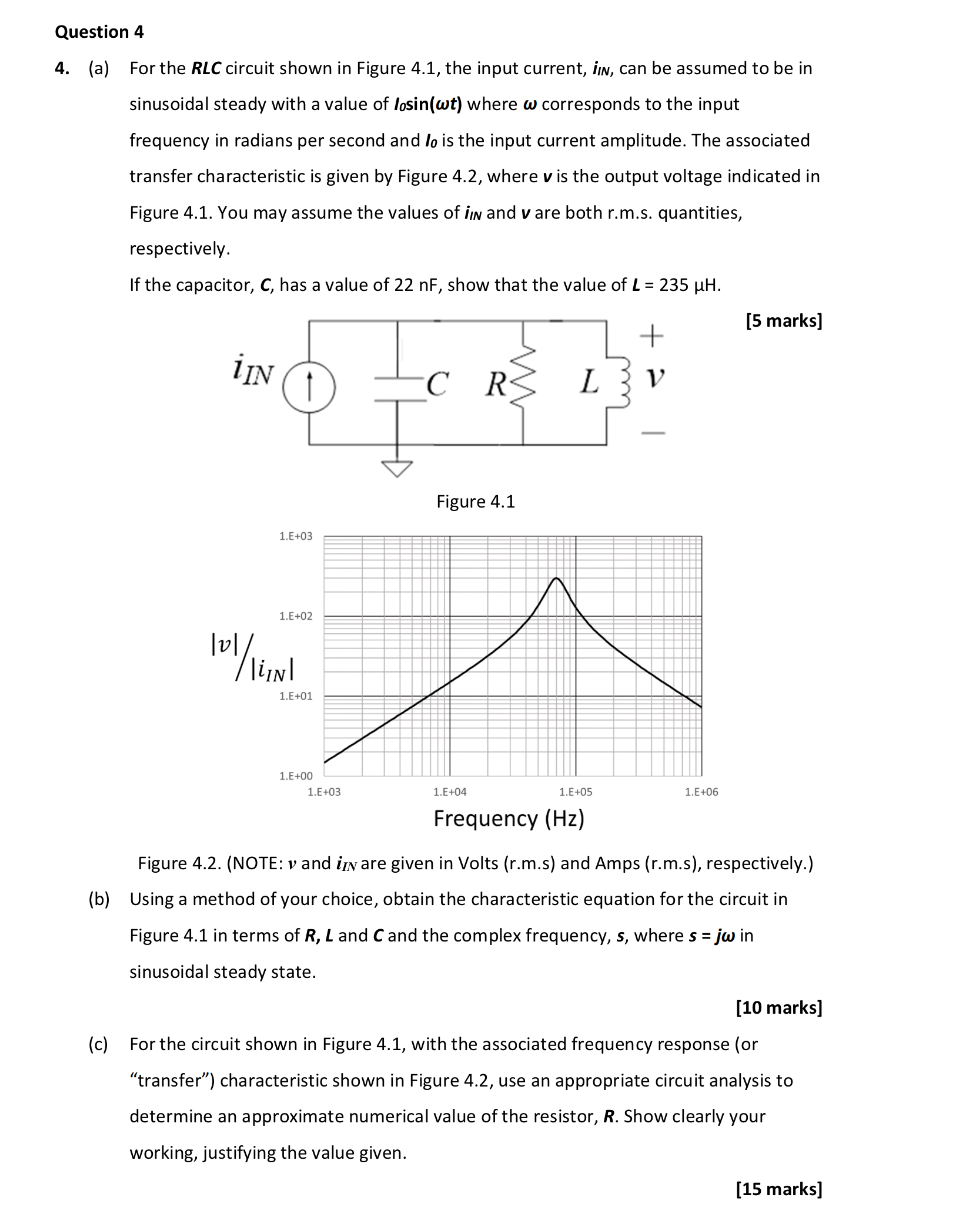
$4.($a$)$ For the RLC circuit shown in Figure $4\mathrm{.}1,$ the input current, $\backslash (\backslash$boldsymbol$\{$i$\}\_\{\backslash$boldsymbol$\{$I$\}\}\backslash ),$ can be assumed to be in sinusoidal steady with a value of $\backslash (\backslash$operatorname$\{$losin$\}(\backslash$omega t$)\backslash )$ where $\backslash (\backslash$omega $\backslash )$ corresponds to the input frequency in radians per second and $\backslash ($ I$\_\{0\}\backslash )$ is the input current amplitude. The associated transfer characteristic is given by Figure $4\mathrm{.}2,$ where $\backslash (\backslash$boldsymbol$\{$v$\}\backslash )$ is the output voltage indicated in Figure $4\mathrm{.}1.$ You may assume the values of $\backslash (\backslash$boldsymbol$\{$i$\}\_\{\backslash$boldsymbol$\{$I$\}\}\backslash )$ and $\backslash (\backslash$boldsymbol$\{$v$\}\backslash )$ are both r$.$m$.$s$.$ quantities, respectively.

If the capacitor, $\backslash (\backslash$boldsymbol$\{$C$\}\backslash ),$ has a value of $22$ nF $,$ show that the value of $\backslash (\backslash$boldsymbol$\{$L$\}=235\backslash$mu $\backslash$mathrm$\{$H$\}\backslash ).$

$[5$ marks$]$

Figire $41$

Figure $4\mathrm{.}2.($NOTE: $\backslash (\backslash$boldsymbol$\{$v$\}\backslash )$ and $\backslash ($ i$\_\{$I N$\}\backslash )$ are given in Volts $($r$.$m$.$s$)$ and Amps $($r$.$m$.$s$),$ respectively.$)$

$($b$)$ Using a method of your choice, obtain the characteristic equation for the circuit in Figure $4\mathrm{.}1$ in terms of $\backslash (\backslash$boldsymbol$\{$R$\},\backslash$boldsymbol$\{$L$\}\backslash )$ and $\backslash (\backslash$boldsymbol$\{$C$\}\backslash )$ and the complex frequency, $\backslash (\backslash$boldsymbol$\{$s$\}\backslash ),$ where $\backslash (\backslash$boldsymbol$\{$s$\}=\backslash$boldsymbol$\{$j$\}\backslash$boldsymbol$\{\backslash$omega$\}\backslash )$ in sinusoidal steady state.

$($c$)$ For the circuit shown in Figure $4\mathrm{.}1,$ with the associated frequency response $($or "transfer"$)$ characteristic shown in Figure $4\mathrm{.}2,$ use an appropriate circuit analysis to determine an approximate numerical value of the resistor, $\backslash (\backslash$boldsymbol$\{$R$\}\backslash ).$ Show clearly your working, justifying the value given.