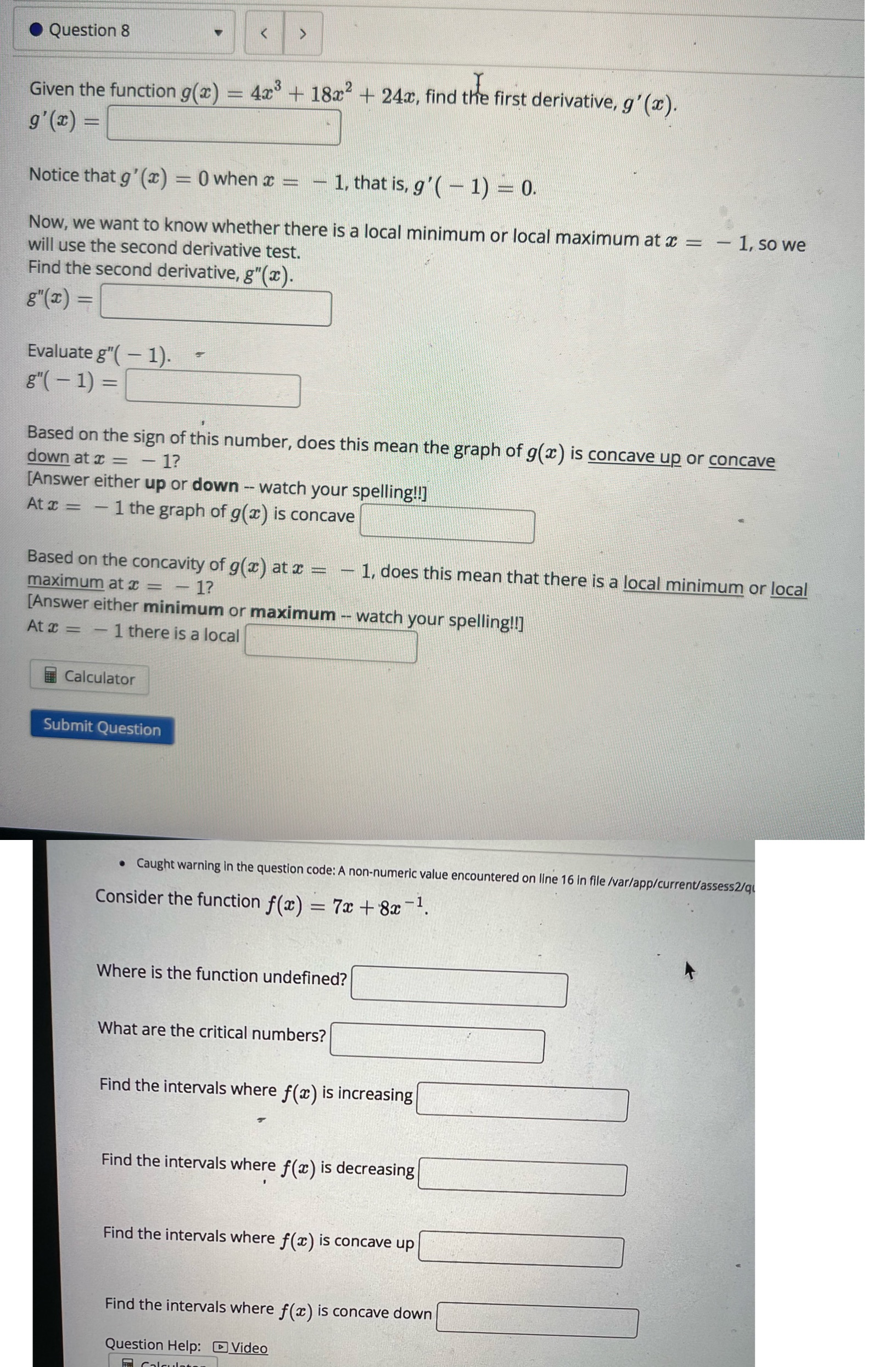
Question 8 Given the function g(x) = 4x3 + 18x2 + 24x, find the first derivative, g' (x). 9' (x) = Notice that g' (x) = 0 when x - - 1, that is, g'( - 1) = 0. Now, we want to know whether there is a local minimum or local maximum at x = - 1, so we will use the second derivative test. Find the second derivative, g"(x). 8" (3 ) = Evaluate g"( - 1). - 8"( - 1) = Based on the sign of this number, does this mean the graph of g(x) is concave up or concave down at x = - 1? [Answer either up or down - watch your spelling!] At x = - 1 the graph of g(x) is concave Based on the concavity of g(x) at x = - 1, does this mean that there is a local minimum or local maximum at x = - 1? [Answer either minimum or maximum -- watch your spelling!!] At x = - 1 there is a local Calculator Submit Question Caught warning in the question code: A non-numeric value encountered on line 16 In file /var/app/current/assess2/qu Consider the function f(x) = 7x + 8x -1. Where is the function undefined? What are the critical numbers? Find the intervals where f() is increasing Find the intervals where f(x) is decreasing Find the intervals where f() is concave up Find the intervals where f(x) is concave down Question Help: Video