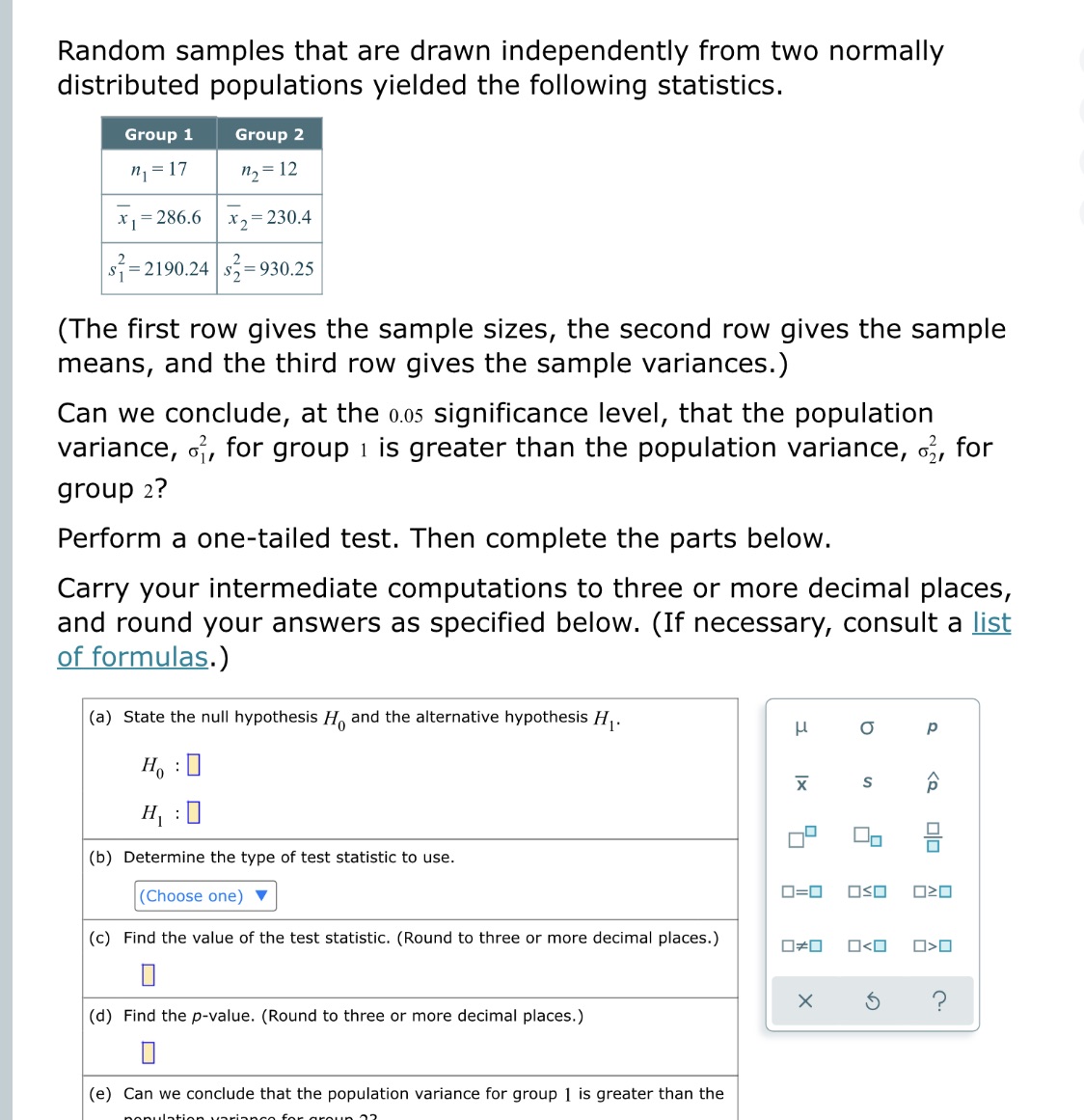
Random samples that are drawn independently from two normally distributed populations yielded the following statistics. Group 1 Group 2 n = 17 n, = 12 x1 = 286.6 x2= 230.4 S = 2190.24 $7 =930.25 (The first row gives the sample sizes, the second row gives the sample means, and the third row gives the sample variances. ) Can we conclude, at the 0.05 significance level, that the population variance, , for group 1 is greater than the population variance, 2, for group 2? Perform a one-tailed test. Then complete the parts below. Carry your intermediate computations to three or more decimal places, and round your answers as specified below. (If necessary, consult a list of formulas.) (a) State the null hypothesis H, and the alternative hypothesis H. O P H : 0 X S H :0 (b) Determine the type of test statistic to use. (Choose one) 0=0 OSO 020 (c) Find the value of the test statistic. (Round to three or more decimal places.) 0*0 00 X 5 (d) Find the p-value. (Round to three or more decimal places.) 0 (e) Can we conclude that the population variance for group 1 is greater than the