Random variable generation with a known density

Assume X is a real random variable with a cumulative distribution function (cdf) F such that for all x R

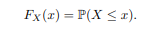
1. Look up the important properties of the function F (continuity, monotonicity, limits, etc.) on Wikipedia and report them here.

2. Demonstrate that the distributions of Y and X are the same. (hint: you can compute cdf of Y , FY (x) = P(Y x).

3. Calculate the cdf of the Cauchy distribution analytically.

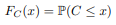
FX(x)=P(Xx) FC(x)=P(Cx) distribution. The equation for the standard Cauchy distribution reduces to f(x)=(1+x2)1