Random Walk.

In lab, we saw how to model the behavior of a random walker on a $2$D grid using a Monte Carlo simulation. In this problem, we will investigate collisions between two of these random walkers. Specifically, we will use our simulation to answer whether a collision is more likely if both walkers are moving or if only one walker is moving.

Part $($a$)$

Start by writing a program to simulate a single random walker on an $\backslash (11\backslash$times $11\backslash )$ grid. Similar to what we discussed in lecture, let this random walker have a $\backslash (20\backslash \%\backslash )$ chance of moving to each orthogonally adjacent cell $($up$,$ down, left, and right$)$ and a $20\backslash \%$ probability of staying still. In order to limit the size of the problem, we will restrict the motion to the confines of our $\backslash (11\backslash$times $11\backslash )$ grid. If the particle tries to move $"$ past" one of the boundaries on its turn, its position does not change $($you can think about this as a particle forfeiting its turn or simply bumping into the wall and staying still$).$

Part $($b$)$

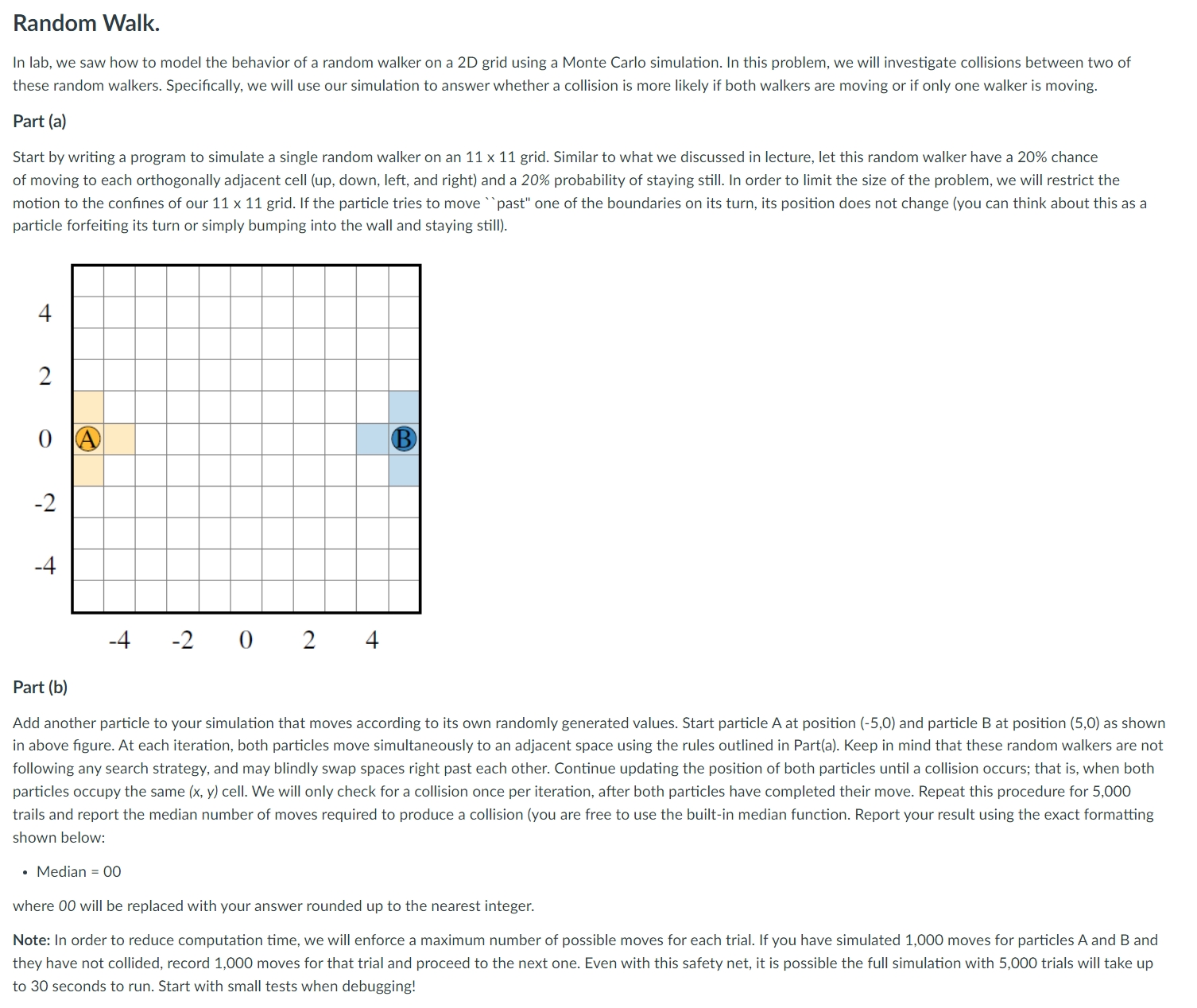
Add another particle to your simulation that moves according to its own randomly generated values. Start particle A at position $(-5,0)$ and particle B at position $(5,0)$ as shown in above figure. At each iteration, both particles move simultaneously to an adjacent space using the rules outlined in Part$($a$).$ Keep in mind that these random walkers are not following any search strategy, and may blindly swap spaces right past each other. Continue updating the position of both particles until a collision occurs; that is$,$ when both particles occupy the same $\backslash (($x$,$ y$)\backslash )$ cell. We will only check for a collision once per iteration, after both particles have completed their move. Repeat this procedure for $5,000$ trails and report the median number of moves required to produce a collision $($you are free to use the built$-$in median function. Report your result using the exact formatting shown below:

$-$ Median $\backslash (=00\backslash )$

where $00$ will be replaced with your answer rounded up to the nearest integer.

Note: In order to reduce computation time, we will enforce a maximum number of possible moves for each trial. If you have simulated $1,000$ moves for particles A and B and they have not collided, record $1,000$ moves for that trial and proceed to the next one. Even with this safety net, it is possible the full simulation with $5,000$ trials will take up to $30$ seconds to run. Start with small tests when debugging!