Question: really need help with problem 1. We are using Fourier Inversion, and Heisenberg for reference. (1) Show that if fe S(R ), then f is

really need help with problem 1. We are using Fourier Inversion, and Heisenberg for reference.

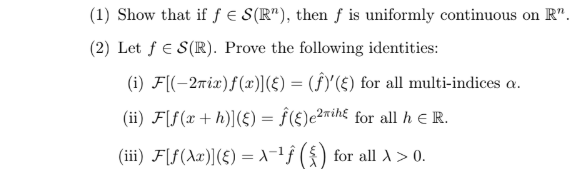
(1) Show that if fe S(R" ), then f is uniformly continuous on R". (2) Let f E S(R). Prove the following identities: (i) F[(-2mix)f()](5) = (f)'({) for all multi-indices a. (ii) F[f(a + h)](8) = f(()e2mine for all he R. (iii) F[f()](8) = x-If for all > > 0

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

Please help me with this assignment, 100% human! Reference book George, J. M. (2024). Contemporary management (12th ed.). McGraw-Hill Education. keiser library Syahbinah, S., & Suhardianto, N....

It is a Complex analysis problem, which requirers fourier transformation to solve it. let u(r, t) be an unknown function with Fourier transform u(w, t) and let f(z) be an arbitrary function that is...

Diagnostic Change Models 1) Leavitt's Model (1965) 2) Weisbord's Six-Box Model (1976) 3) Congruence Model for Organization Analysis (1977) 4) McKinsley 7-S Model (1982) 4) Tichy's Technical Political...

re Regular Languages and Finite Automata (a) Let L be the set of all strings over the alphabet {a, b} that end in a and do not contain the substring bb. Describe a deterministic finite automaton...

List and briefly define all quantitative measures and statistics (e.g., sample size, number of groups, number of treatments, standard deviation, standard error, mean, intercept, slope, F statistic,...

What are the Statistics Mentioned? Sample Size (n): Number of Groups: Number of Treatments: Standard Deviation (): Standard Error: Mean (): F Statistic: Degrees of Freedom (df): P-Value: An ANOVA...

Describe the quantitative results of the study, including all statistics, identified in the article? Describe the meaning of the results and how they answer the research question? An ANOVA approach...

Final Paper Instructions/Guidelines: The final paper must be a minimum of 5 pages and a maximum of 7 pages in APA format. You can find APA guidelines in the Week Six folder under final paper tips....

Fill-in the blank. Using algebraic substitution, the f x?Vx + 3dx equals 2/(x + 3)3 +3) _ 6(x+3) |+c. +. 7 3 . x+3 . . 3 D. 3(x + 3)2

Suppose that a firm engages in a derivative transaction that qualifies for fair value hedging? The firm holds a security and hedges it by selling a derivative. During the course of the hedge, the...

Under current Federal estate tax law: a . If the bypass amount is used, the deduction for charitable contributions is not allowed. b . The bypass amount is portable. c . Disclaimers cannot be used to...

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...