Rebalance function for binary search tree:

programming language c++;

void rebalance

{

//code here

}

(1) Rebalance

binary search tree with the left leaning red black technique. 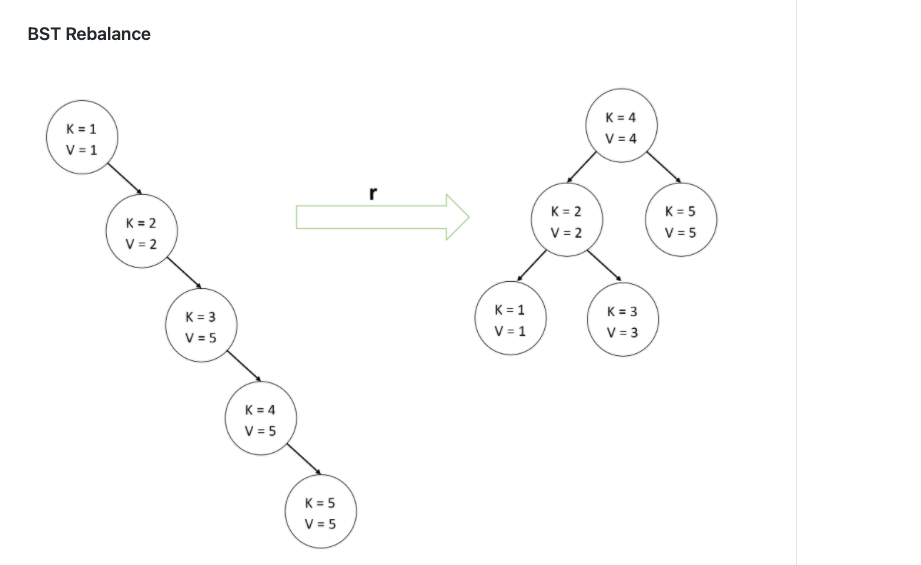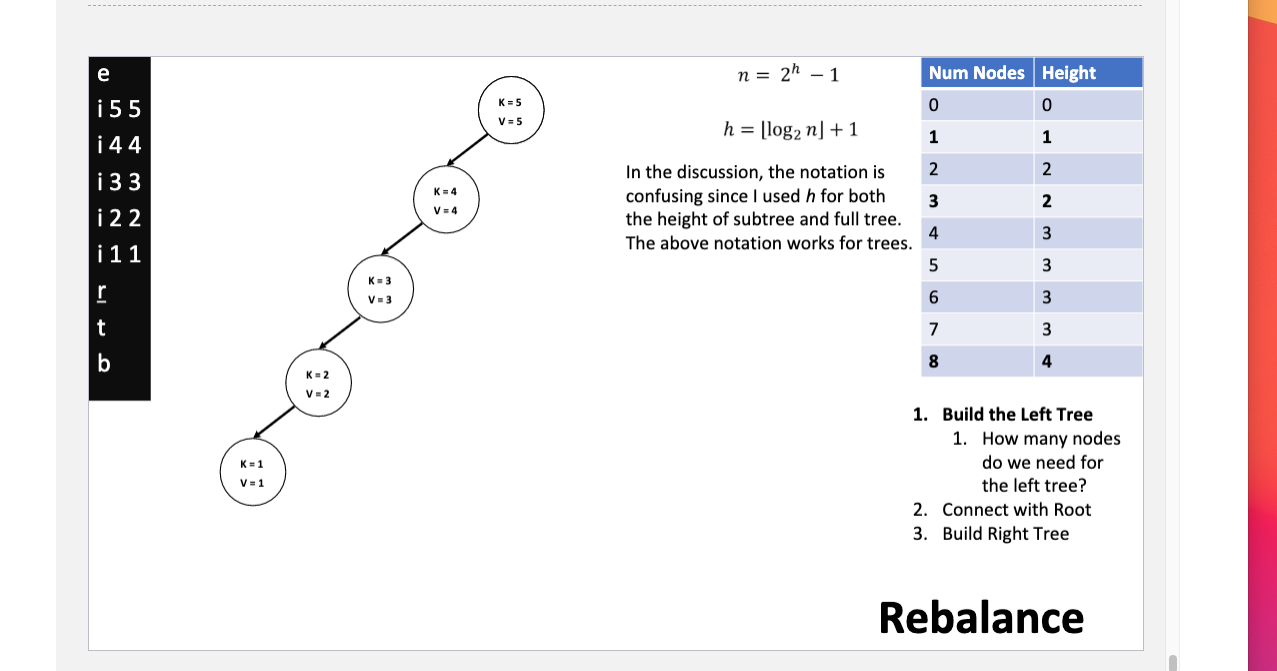Pseudo code given for help of implementation:

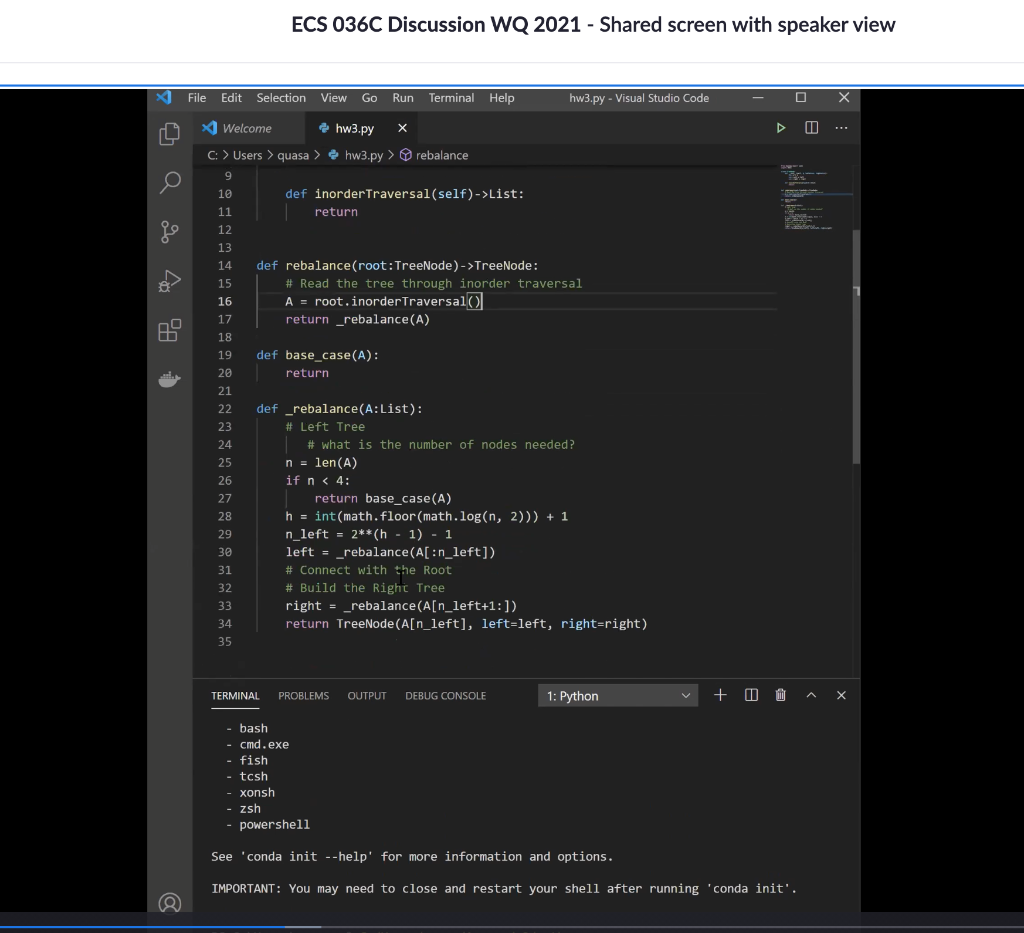
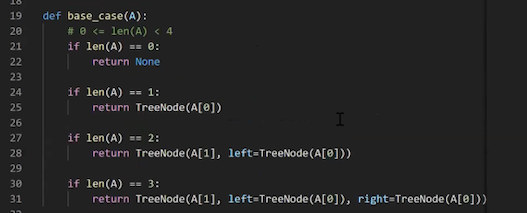
Where A, is a vector/list containing all of the trees nodes in order. and h is height of the tree.

BST Rebalance K = 1 V = 1 K = 4 V = 4 K = 2 V = 2 K = 2 V = 2 K = 5 V = 5 K = 3 V = 5 K = 1 V=1 K = 3 V = 3 K = 4 V = 5 K = 5 V = 5 e n = 2h - 1 Num Nodes Height K = 5 V=5 0 0 h = [log2 n] + 1 1 1 2 2. i 55 i 44 i 33 i 22 i 11 In the discussion, the notation is confusing since I used h for both the height of subtree and full tree. The above notation works for trees. 3 2 V=4 4 3 5 3 K = 3 r V-3 6 3 t 7 3 b 8 4 K-2 V=2 1. Build the Left Tree 1. How many nodes do we need for the left tree? 2. Connect with Root 3. Build Right Tree Rebalance ECS 036C Discussion WQ 2021 - Shared screen with speaker view Q t File Edit Selection View Go Run Terminal Help hw3.py - Visual Studio Code Welcome hw3.py x C: > Users > quasa > hw3.py > rebalance 9 10 def inorderTraversal(self)->List: 11 return 12 13 14 def rebalance (root:TreeNode)->TreeNode: 15 # Read the tree through inorder traversal 16 A = root.inorder Traversal() 17 return _rebalance(A) 18 19 def base_case(A): 20 return 21 22 def _rebalance(A:List): 23 # Left Tree 24 # what is the number of nodes needed? 25 n = len(A) 26 if n Users > quasa > hw3.py > rebalance 9 10 def inorderTraversal(self)->List: 11 return 12 13 14 def rebalance (root:TreeNode)->TreeNode: 15 # Read the tree through inorder traversal 16 A = root.inorder Traversal() 17 return _rebalance(A) 18 19 def base_case(A): 20 return 21 22 def _rebalance(A:List): 23 # Left Tree 24 # what is the number of nodes needed? 25 n = len(A) 26 if n