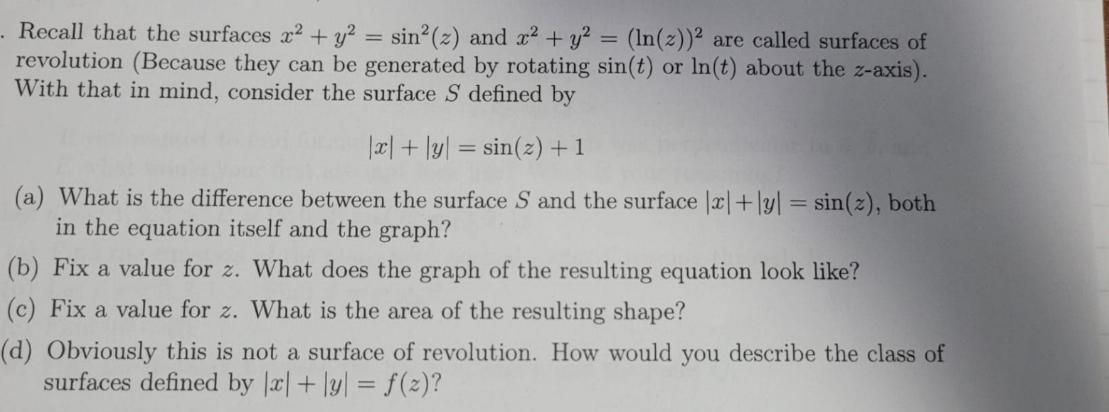
. Recall that the surfaces x + y = sin (z) and x + y = (ln(z)) are called surfaces of revolution (Because they can be generated by rotating sin(t) or ln(t) about the z-axis). With that in mind, consider the surface S defined by |x + y = sin(z) + 1 (a) What is the difference between the surface S and the surface |x|+|y| = sin(z), both in the equation itself and the graph? (b) Fix a value for z. What does the graph of the resulting equation look like? (c) Fix a value for z. What is the area of the resulting shape? (d) Obviously this is not a surface of revolution. How would you describe the class of surfaces defined by |x| + y = f(z)?