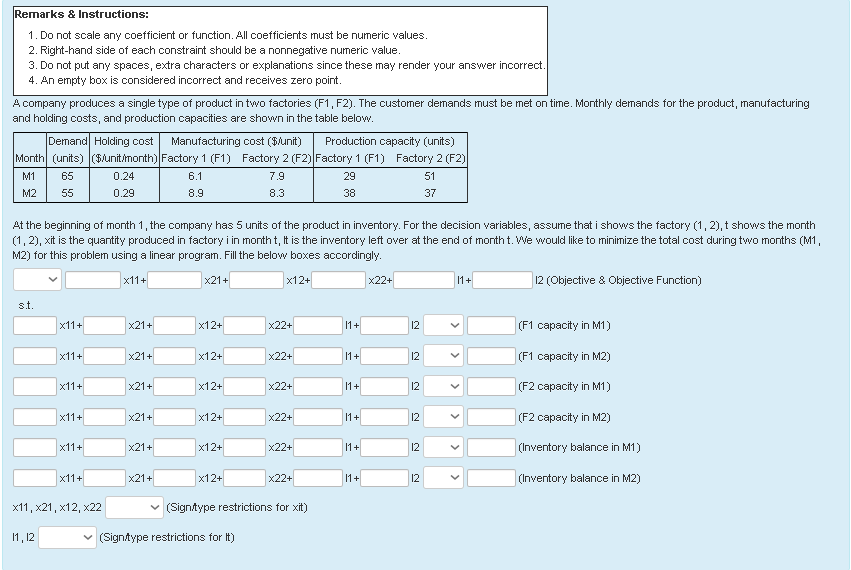
Remarks & Instructions: 1. Do not scale any coefficient or function. All coefficients must be numeric values. 2. Right-hand side of each constraint should be a nonnegative numeric value. 3. Do not put any spaces, extra characters or explanations since these may render your answer incorrect. 4. An empty box is considered incorrect and receives zero point. A company produces a single type of product in two factories (F1,F2). The customer demands must be met on time. Monthly demands for the product, manufacturing and holding costs, and production capacities are shown in the table below. Demand Holding cost Manufacturing cost ($/unit) Production capacity (units) Month (units) ($/unit/month) Factory 1 (F1) Factory 2 (F2) Factory 1 (F1) Factory 2 (F2) 0.24 7.9 29 51 M2 M1 6.1 65 55 0.29 8.9 8.3 38 37 At the beginning of month 1, the company has 5 units of the product in inventory. For the decision variables, assume that i shows the factory (1, 2),t shows the month (1,2), xit is the quantity produced in factory i in month t, it is the inventory left over at the end of month t. We would like to minimize the total cost during two months (M1, M2) for this problem using a linear program. Fill the below boxes accordingly. x11+ X21+ x12+ X22+ 11+ 12 (Objective & Objective Function) St. x11+ X21+ x12+ x22+ 11+ 12 (Inventory balance in M1) x11+ X21+ x12+ x22+ 11+ 12 (Inventory balance in M2) x11,x21, X12, X22 (Sign:type restrictions for xit) 11, 12 (Sign:type restrictions for it) Remarks & Instructions: 1. Do not scale any coefficient or function. All coefficients must be numeric values. 2. Right-hand side of each constraint should be a nonnegative numeric value. 3. Do not put any spaces, extra characters or explanations since these may render your answer incorrect. 4. An empty box is considered incorrect and receives zero point. A company produces a single type of product in two factories (F1,F2). The customer demands must be met on time. Monthly demands for the product, manufacturing and holding costs, and production capacities are shown in the table below. Demand Holding cost Manufacturing cost ($/unit) Production capacity (units) Month (units) ($/unit/month) Factory 1 (F1) Factory 2 (F2) Factory 1 (F1) Factory 2 (F2) 0.24 7.9 29 51 M2 M1 6.1 65 55 0.29 8.9 8.3 38 37 At the beginning of month 1, the company has 5 units of the product in inventory. For the decision variables, assume that i shows the factory (1, 2),t shows the month (1,2), xit is the quantity produced in factory i in month t, it is the inventory left over at the end of month t. We would like to minimize the total cost during two months (M1, M2) for this problem using a linear program. Fill the below boxes accordingly. x11+ X21+ x12+ X22+ 11+ 12 (Objective & Objective Function) St. x11+ X21+ x12+ x22+ 11+ 12 (Inventory balance in M1) x11+ X21+ x12+ x22+ 11+ 12 (Inventory balance in M2) x11,x21, X12, X22 (Sign:type restrictions for xit) 11, 12 (Sign:type restrictions for it)