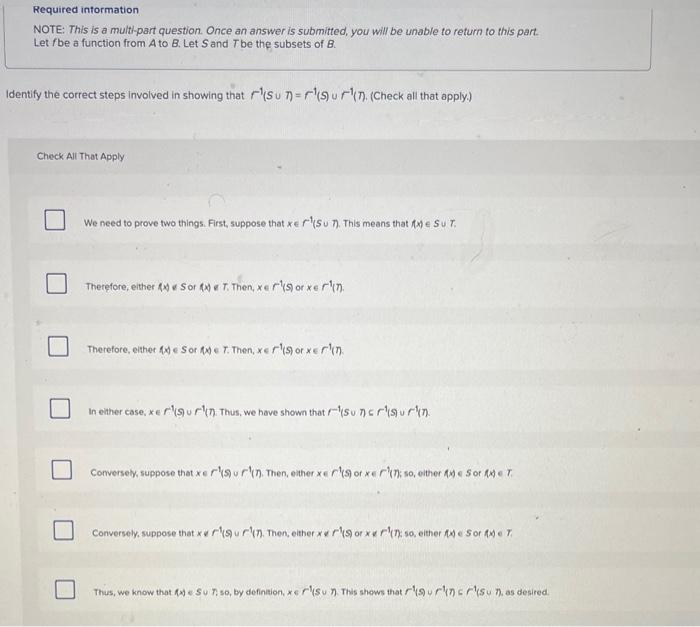
Required intormation NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Let f be a function from A to B, Let S and T be the subsets of B. Identify the correct steps involved in showing that f1(ST)=f1(S) u f1(T). (Check all that apply.) Check All That Apply We need to prove two things. First, suppose that xf1(ST). This means that f(x)ST. Therefore, either f(x)&S or f(x)T. Then, xr1(S) or xr1(n. Therefore, ether {x)S or {x)T. Then, xf1(S) or xf1(n. In either case, xf1(S)r1(n). Thus, we have shown that r1(Sn)r1(S)r1(n). Conversety, suppose that xr1(S) o r1(n). Then, ether xr1(S) or xr1(7; so, elther Ax) e sor f(x)r. Conversely, suppose that xr1(S) o r1(). Then, either x&r1(S) or xr1(T) so, either Ax) e s or fx) e T. Thus, we know that fx e su so, by definaion, x \& r1( su n. This shews that r1(9 u r1(7)sr1(S u , as desired