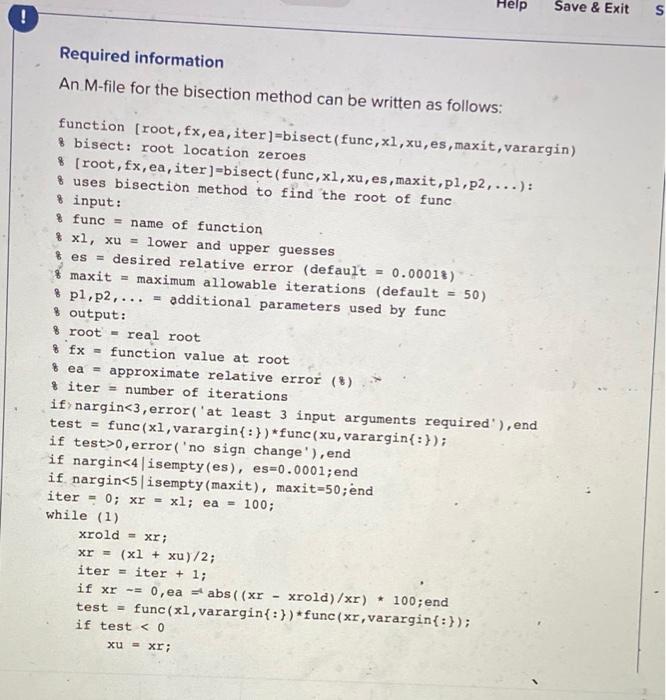
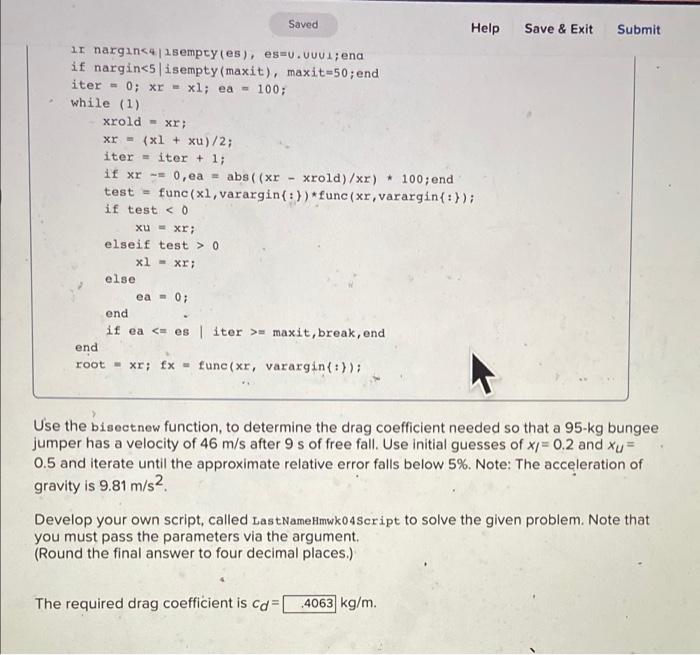
Save & Exit ! S Required information An M-file for the bisection method can be written as follows: function [root, fx, ea, iter ]=bisect(func,xl, xu, es,maxit, varargin) 8 bisect: root location zeroes $ (root, fx, ea, iter)=bisect(func,xl, xu, es,maxit,pl,p2, ...): % uses bisection method to find the root of func $ input: func = name of function % xl, xu = lower and upper guesses es = desired relative error (default 0.00018) % maxit = maximum allowable iterations (default = 50) pl,p2,... = additional parameters used by func $output: 8 root- real root 8 fx= function value at root % ea = approximate relative error (8) * iter = number of iterations if nargin0, error('no sign change'), end if nargin 0 xl xr; else ea = 0; end if ea maxit, break, end end root - xr; fx - func(xr, varargin{:}); Use the bisectnew function, to determine the drag coefficient needed so that a 95-kg bungee jumper has a velocity of 46 m/s after 9 s of free fall. Use initial guesses of x = 0.2 and xv= 0.5 and iterate until the approximate relative error falls below 5%. Note: The acceleration of gravity is 9.81 m/s2 Develop your own script, called LastName Hmwk04Script to solve the given problem. Note that you must pass the parameters via the argument. (Round the final answer to four decimal places.) The required drag coefficient is cd= [ 4063 kg/m