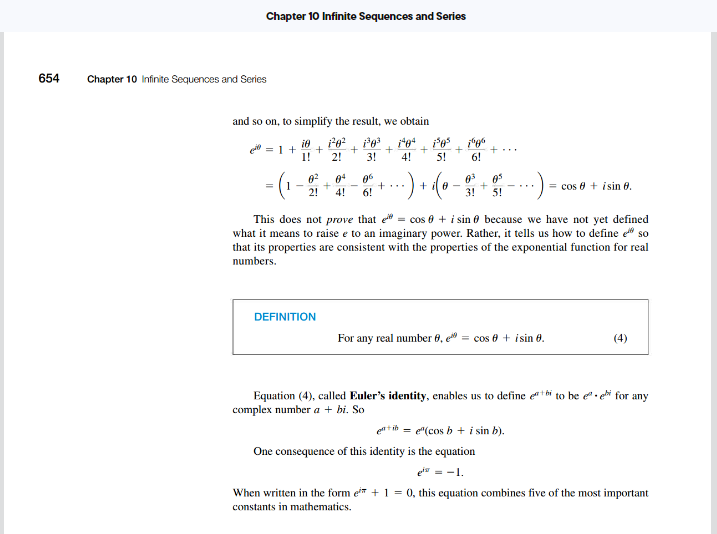
Section 10.10 Reading Assignment: Applications of Taylor Series Instructions. Read through this assignment and complete the three exercises below by reading the appropriate passages of the textbook. We have three main applications of Taylor series in this section: (1) expressing nonelementary integrals as power series and using partial sums to approximate their values, (2) evaluating limits, and (3) deducing formulas from power series representations. Exercise 1. Read the subsection "Nonelementary Integrals" (p. 650 - 651). Explain how the power series for the integral (sin(x) dx is found and how this is used to estimate the definite integral sin x dx. Also, explain how the error bound is used in Example 4. The subsection "Arctangents" (p. 651 - 652) extends this idea to show how we can we find a good approximation of pi without too much computational effort. We'll stick to more basic examples, but this section might be of interest to the curious. Exercise 2. Read Example 6 (p. 652 - 653). Based on this example, explain how Taylor series can be used to compute limits. Exercise 3. Read the subsection "Euler's Identity" (p. 653 - 654). State what Euler's identity is and explain how the textbook obtains it. Take a look at Table 10.1 (p. 654), which contains all the "common" Taylor series. This table might be worth having for reference. Many of these may be expected to be known for the assignments and final exam. 1 I've heard that this is the main method for computing limits instead of l'Hpitals rule in Europe. Personally, while I find this method of computing limits useful, it's also a bit of a mess to write out (at least without Big O or little o notation). 2 This last result hints at some connection between complex numbers, calculus, and power series. Unfortunately, we will not develop these ideas here, but there's certain something there, which is covered in complex analysis. 650 Chapter 10 Infinite Sequences and Series Chapter 10 Infinite Sequences and Series EXAMPLE 2 We know from Section 3.11, Example 1, that 1 + x = 1 + (x/2) for x small. With m = 1/2, the binomial series gives quadratic and higher-order approximations as well, along with error estimates that come from the Alternating Series Estimation Theorem: (1 + x)/2 = 1 + + + () (0-0, (X-IX-9), 2! 3! (4)(-4)(-2)(-2) 4! =1+ + 2 8 16 128 +... Substitution for x gives still other approximations. For example, 1 - 1- 2 for x| small 8 - for small, that is, |x| large. 2r &r Evaluating Nonelementary Integrals Sometimes we can use a familiar Taylor series to find the sum of a given power series in terms of a known function. For example, 10 3! + 5! x14 7! + --=(x) (12)+ (x2)5_ (x2)7 sin.x. 3! 5! 7! Additional examples are provided in Exercises 59-62. Taylor series can be used to express nonelementary integrals in terms of series. Inte- grals like sin x dx arise in the study of the diffraction of light. EXAMPLE 3 Express sin x dx as a power series. Solution From the series for sin x we substitute x for x to obtain sin x = x - 10 x x14 18 + + 3! 5! 7! 9! Therefore, sin x dx = C+ x15 x19 - + 7.3! 11.5! 15.7! 19.9! + EXAMPLE 4 Estimate sin x dx with an error of less than 0.001. Solution From the indefinite integral in Example 3, we easily find that J'sin x dx = 1 7 dx = 13 - 7' 31 + 11' 5! - 15' 71+19-91 }} 11.5! 15.7! The series on the right-hand side alternates, and we find by numerical evaluations that 1 0.00076 11.5! Chapter 10 Infinite Sequences and Series 10.10 Applications of Taylor Series 651 is the first term to be numerically less than 0.001. The sum of the preceding two terms gives L' 1 1 sin x dx - 0.310. 42 With two more terms we could estimate L'sin x sin x2 dx 0.310268 with an error of less than 10%. With only one term beyond that we have J'si sin x dx 1 1 1 + 42 1320 1 75600 6894720 0.310268303, with an error of about 1.08 x 10%. To guarantee this accuracy with the error formula for the Trapezoidal Rule would require using about 8000 subintervals. Arctangents In Section 10.7, Example 5, we found a series for tanx by differentiating to get 1 -tan'x= = 1 x + x^ 15 + ... 1+x and then integrating to get tan x =x- + - However, we did not prove the term-by-term integration theorem on which this conclu- sion depended. We now derive the series again by integrating both sides of the finite formula 1+ (-1)+12+2 1+2 (2) in which the last term comes from adding the remaining terms as a geometric series with first term a = (-1)+12+2 and ratio r = 1. Integrating both sides of Equation (2) from 1 = 0 to f = x gives tan x-x- + 5 7 + + (-1)" 2n+1 + R(x). where R(x)= *(-1)+12+2 -dt. 1+12 0 The denominator of the integrand is greater than or equal to 1; hence \R, (x) = Pa+2 dt = x|2013 211 + 3 If x 1, the right side of this inequality approaches zero as noo. Therefore lim-R,,(x) = 0 if |x| 1 and tanx= (-1)+1 21' x tanx-x- + - 3 5 |x| 1. (3) 17 7 |x| 1. 652 Chapter 10 Infinite Sequences and Series Chapter 10 Infinite Sequences and Series We take this route instead of finding the Taylor series directly because the formulas for the higher-order derivatives of tanx are unmanageable. When we put x = 1 in Equa- tion (3), we get Leibniz's formula: + (-1)" 2n+1+ Because this series converges very slowly, it is not used in approximating to many deci- mal places. The series for tanx converges most rapidly when x is near zero. For that reason, people who use the series for tanx to compute use various trigonometric identities. then For example, if atan 1/2 and B = tan 3' tan (a + B) = tana + tan -tan a tan = = 1 =tan and therefore =a+B=tan+tan 3 Now Equation (3) may be used with x = 1/2 to evaluate tan (1/2) and with x= 1/3 to give tan (1/3). The sum of these results, multiplied by 4, gives . Evaluating Indeterminate Forms We can sometimes evaluate indeterminate forms by expressing the functions involved as Taylor series. EXAMPLE 5 Evaluate In x lim Solution We represent In x as a Taylor series in powers of x-1. This can be accom- plished by calculating the Taylor series generated by In x at x 1 directly or by replacing x by x-1 in the series for In(1 + x) in Section 10.7, Example 6. Either way, we obtain - In x = (x 1)-2(x 1) + from which we find that In x lim = lim 1- - 1) + 31 = 1. Of course, this particular limit can be evaluated using l'Hpital's Rule just as well. EXAMPLE 6 Evaluate sin x-tan x lim 110 Chapter 10 Infinite Sequences and Series 10.10 Applications of Taylor Series 653 Solution The Taylor series for sin x and tan.x, to terms in x, are sin x - x + 3! 5! tan x = x + + x 2x 3 15 Subtracting the series term by term, it follows that -- sin x-tan x=- = *(1--...). Division of both sides by x and taking limits then gives sin x-tan x 1 lim x-0 lim == 01-2 8 If we apply series to calculate lim,((1/sin x) - (1/x)), we not only find the limit successfully but also discover an approximation formula for esc.x. EXAMPLE 7 Find lim 0 sin.x Solution Using algebra and the Taylor series for sin x, we have x x- + 1 1 --= sin x x x - sin x xsin x 3! 5! x+ x- + 3! 5! 3! - -lai 1 3! 5! x" + 1- 3! Therefore, 1 3! lim - - lim sin x 1-0 1- From the quotient on the right, we can see that if |x| is small, then = 0. 1 1 1 x = or sin x x 3! 6 CSC x = + x 6' Euler's Identity A complex number is a number of the form a + bi, where a and b are real numbers and i = V-I (see Appendix 7). If we substitute x = 10 (real) in the Taylor series for e* and use the relations = -1, i = 1 = -i, i+= = 1, i = i'i = i, 654 Chapter 10 Infinite Sequences and Series Chapter 10 Infinite Sequences and Series = 1 + + 1! 2! and so on, to simplify the result, we obtain i0 120 1303 1404 1505 + 3! 4! + + + +... 5! 6! 02 04 06 = 1- + +... 2! 4! 6! ...) + (0. 03 + 3! 5! = cos + isin 6. This does not prove that ecos + i sin because we have not yet defined what it means to raise e to an imaginary power. Rather, it tells us how to define e so that its properties are consistent with the properties of the exponential function for real numbers. DEFINITION For any real number 8, ecos + isin 0. (4) Equation (4), called Euler's identity, enables us to define ethi to be e ei for any complex number a + bi. So eibe"(cos b + i sin b). One consequence of this identity is the equation ex = -1. When written in the form ei + 1 = 0, this equation combines five of the most important constants in mathematics. TABLE 10.1 Frequently Used Taylor Series 1 1-x =1+x+x + = |x|