Question: Section 2.1 Integrating Factor: Problem 1 (1 point) Find the general solution, y(t), which solves the problem below, by the method of integrating factors. 7t-

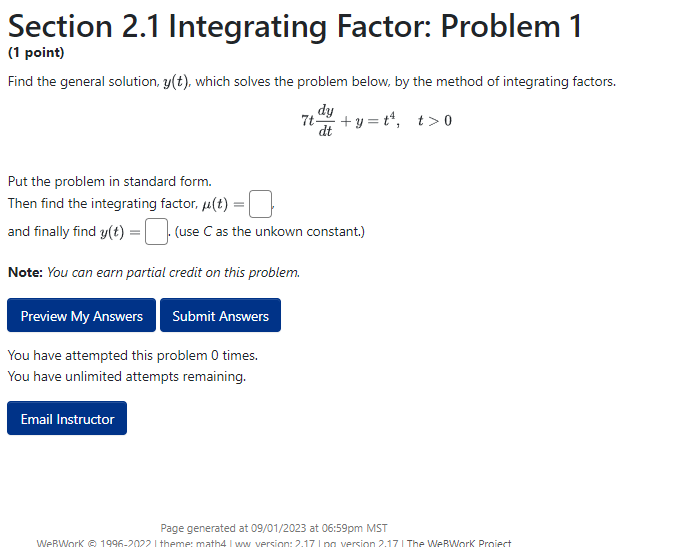
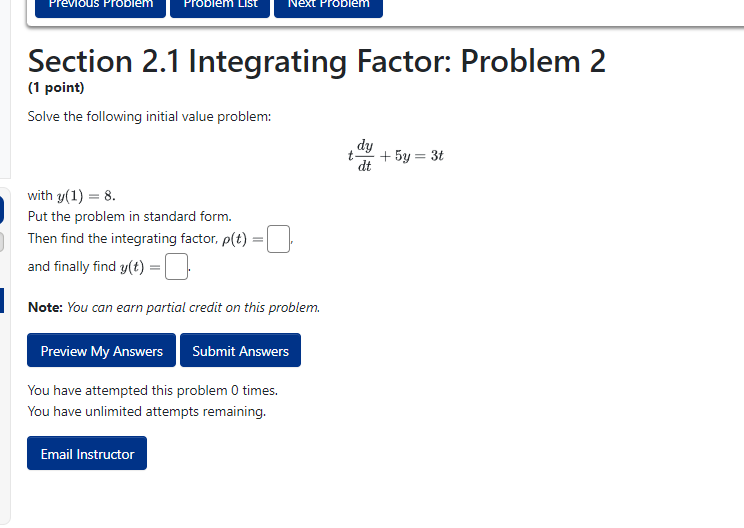
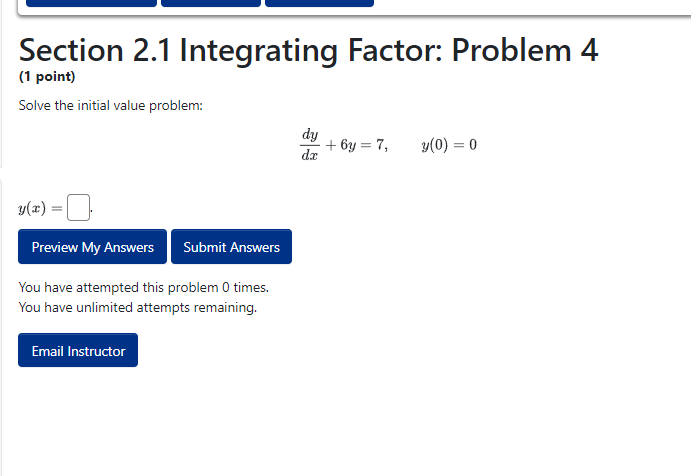
Section 2.1 Integrating Factor: Problem 1 (1 point) Find the general solution, y(t), which solves the problem below, by the method of integrating factors. 7t- dy dt ty=t, t>0 Put the problem in standard form. Then find the integrating factor, u(t) = and finally find y(t) = . (use C as the unkown constant.) Note: You can earn partial credit on this problem. Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining. Email Instructor Page generated at 09/01/2023 at 06:59pm MST 10 1996-2027 1 th 1217 | The WeBWork ProSection 2.1 Integrating Factor: Problem 2 {1 point} Solve the following initial value problem: t + F! = 3: {it J'J with ml] 3. I Put the problem in standard form. Then find the integrating factor. {:{tj I I. andfinallyfindyIt] | |. I Note: You can earn portion! credit on this problem. Preview My Answers Submit Answers too have attempted this problem El times. You have unlimited attempts remaining. Email Instructor Section 2.1 Integrating Factor: Problem 3 (1 point) Find the general solution to the differential equation dy r' + 2xy +x = 0 Put the problem in standard form. Find the integrating factor, p(*) = Find y(@) = Use C as the unknown constant. Note: You can earn partial credit on this problem. Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining. Email Instructor Page generated at 09/01/2023 at 06:59pm MST WeBWork @ 1996-2022 | theme: math4 | ww_version: 2.17 | pg_version 2.17 | The WeBWork ProjectSection 2.1 Integrating Factor: Problem 4 [1 point} Solve the initial value problem: \"sir-ll l |- Preview My Answers Submit Answers You have attempted this problem CI times. You have unlimited attempts remaining. Email Instructor

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

(1 point) Find the general solution, y(t), which solves the problem below, by the method of integrating factors. 5t- dy dt ty = t, t>0 Put the problem in standard form. Then find the integrating...

Thank you for the help (1 point) Find the general solution, y(t), which solves the problem below, by the method of integrating factors. 5t- dy dt ty = t, t>0 Put the problem in standard form. Then...

MAT244 - Ordinary Differential Equations - Summer 2016 Assignment 1 Due: June 8, 2016 Full Name: Last First Student #: Indicate which Tutorial Section you attend by filling in the appropriate circle:...

Solve the initial value problem dx dt with x(0) = -2. x(t): = - 4x = cos(2t) (1/10)(sin2t-2cos2t)-(9/5)(e^(4t))

This comes from the textbook Differential Equations and Linear Algebra 4th edition. Find the solution of the initial value problem. dq dz = 4 + sin z, and q = 8 when z = 0. q(2) =(3) Consider the...

EGM 6321 Due 11/24/2015 Homework 8 1. Consider the linear autonomous system dx 2x 7 y dt dy 3x 8 y dt a) Determine the nature of the critical point of the system b) Find the general solution: x=x(t),...

7. [-3 Points] DETAILS ZILLDIFFEQMODAP11 2.3.017. MY NOTES ASK YOUR TEACHER Find the general solution of the given differential equation. cos(x) E + (sin(x))y = 1 dx eel l Give the largest interval...

I am working on a homework problem and am stumped on part B. Kim hotels is interested in developing a new hotel in seoul. The company estimates that the hotel would require an initial investment of...

step by step please Find the general solution, y(t), which solves the problem below, by the method of integrating factors. dy 4t _+_ y Put the problem in standard form. Then find the integrating...

write some parts that are (result, discussion and conclusion) after understanding thesis idea and literature review present in the same thesis. 2-Refining and treatment all thesis including...

The DuPont identity presented in the chapter is commonly referred to as the three- factor DuPont identity. Another common way that the DuPont identity is expressed is the five- factor model, which...

Whindor Compary has been in buniness weveral years at the end of the current vear the unadfunt hed balaves show: \ table [ [ Acrounta Recrelvible,$ 7 7 8 2 0 0 ] , [ Sales Remene, 2 . 4 8 4 9 0 0 ] ,...

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...