Show that at most one node in an AVL tree becomes unbalanced after operation removeAboveExternal is performed within the execution of a remove operation.

Note: If one of the children of node w is an external node, say node z, we simply remove w and z from T, and replace w with the sibling of z (which is an operation called removeAboveExternal(z)

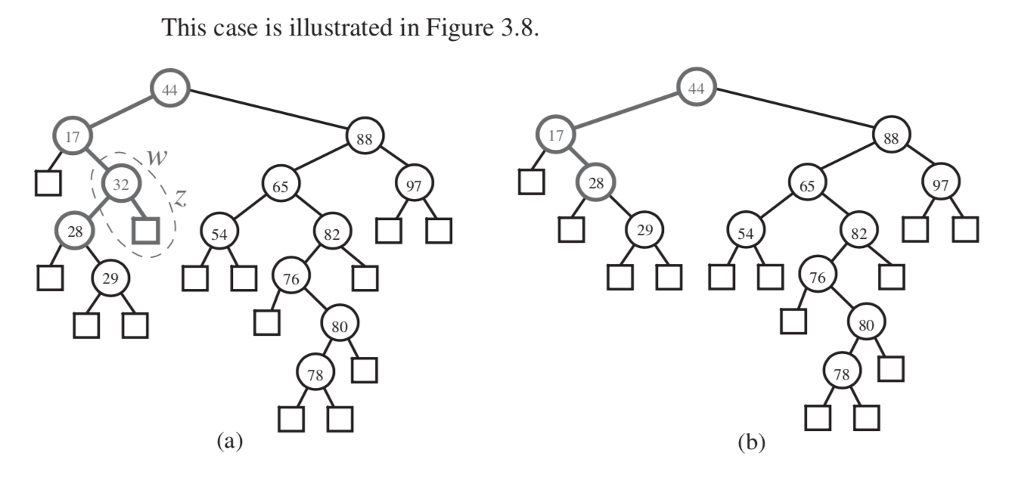
This case is illustrated in Figure 3.8. 17 17 65 97 28 65 97 Z. 28 54 82 29 54 82 29 76 76 80 80 78 78